okama.Portfolio

class Portfolio(assets=None, *, first_date=None, last_date=None, ccy='USD', inflation=True, weights=None, rebalancing_period='month', initial_amount=1000.0, cashflow=0, discount_rate=None, symbol=None)

Bases: ListMaker

Implementation of investment portfolio.

Investments portfolio is a type of financial asset (same as stocks, ETF, mutual funds, currencies etc.). Arguments are similar to AssetList, however Portfolio additionally has:

weights
rebalancing_period
initial_amount
cashflow
discount_rate
symbol

Portfolio is defined by the investment strategy, which includes: - asset allocation (financial assets and their proportions in the portfolio) - the initial investment (initial_amount parameter) - cash flows or withdrawals/contributions (cashflow parameter) - discount rate (discount_rate parameter) - the rebalancing strategy (rebalancing_period parameter)

The rebalancing is the action of bringing the portfolio that has deviated away from original target asset allocation back into line. After rebalancing the portfolio assets have original weights.

Parameters:

assetslist, default None: List of assets. Could include tickers or asset like objects (Asset, Portfolio). If None a single asset list with a default ticker is used.
first_datestr, default None: First date of monthly return time series. If None the first date is calculated automatically as the oldest available date for the listed assets.
last_datestr, default None: Last date of monthly return time series. If None the last date is calculated automatically as the newest available date for the listed assets.
ccystr, default ‘USD’: Base currency for the list of assets. All risk metrics and returns are adjusted to the base currency.
inflation: bool, default True: Defines whether to take inflation data into account in the calculations. Including inflation could limit available data (last_date, first_date) as the inflation data is usually published with a one-month delay. With inflation = False some properties like real return are not available.
weightslist of float, default None: List of assets weights. The weight of an asset is the percent of an investment portfolio that corresponds to the asset. If weights = None an equally weighted portfolio is created (all weights are equal).
rebalancing_period{‘none’, ‘month’, ‘quarter’, ‘half-year’, ‘year’}, default ‘month’: Rebalancing period (rebalancing frequency) is predetermined time intervals when the investor rebalances the portfolio. If ‘none’ assets weights are not rebalanced.
initial_amountfloat, default 1000: Portfolio initial investment FV (at last_date).
cashflowfloat, default 0: Portfolio monthly cash flow FV (at last_date). Negative value corresponds to withdrawals. Positive value corresponds to contributions. Cash flow value is indexed each month by inflation.
discount_ratefloat or None, default None: Cash flow discount rate required to calculate PV values. If not provided geometric mean of inflation is taken. For portfolios without inflation the default value from settings is used.
symbolstr, default None: Text symbol of portfolio. It is similar to tickers but have a namespace information. Portfolio symbol must end with .PF (all_weather_portfolio.PF). If None a random symbol is generated (portfolio_7802.PF).

Methods & Attributes

`annual_return_ts`	Calculate annual rate of return time series for portfolio.
`assets_close_monthly`	Show assets monthly close time series adjusted to the base currency.
`assets_dividend_yield`	Calculate last twelve months (LTM) dividend yield time series (monthly) for each asset.
`close_monthly`	Portfolio size monthly time series.
`currency`	Return the base currency of the Asset List.
`describe`([years])	Generate descriptive statistics for the portfolio.
`discount_rate`	Return portfolio cash flow discount rate.
`diversification_ratio`	Calculate Diversification Ratio for the portfolio.
`dividend_yield`	Calculate last twelve months (LTM) dividend yield time series for the portfolio.
`dividend_yield_annual`	Calculate last twelve months (LTM) dividend yield annual time series.
`dividends`	Calculate portfolio dividends monthly time series.
`dividends_annual`	Return calendar year dividends sum time series for each asset.
`drawdowns`	Calculate drawdowns time series for the portfolio.
`get_cagr`([period, real])	Calculate portfolio Compound Annual Growth Rate (CAGR) for a given trailing period.
`get_cumulative_return`([period, real])	Calculate cumulative return over a given trailing period for the portfolio.
`get_cvar_historic`([time_frame, level])	Calculate historic Conditional Value at Risk (CVAR, expected shortfall) for the portfolio.
`get_rolling_cagr`([window, real])	Calculate rolling CAGR (Compound Annual Growth Rate) for the portfolio.
`get_rolling_cumulative_return`([window, real])	Calculate rolling cumulative return.
`get_sharpe_ratio`([rf_return])	Calculate Sharpe ratio.
`get_sortino_ratio`([t_return])	Calculate Sortino ratio for the portfolio with specified target return.
`get_var_historic`([time_frame, level])	Calculate historic Value at Risk (VaR) for the portfolio.
`jarque_bera`	Perform Jarque-Bera test for normality of portfolio returns time series.
`kstest`([distr])	Perform one sample Kolmogorov-Smirnov test on portfolio returns and evaluate goodness of fit for a given distribution.
`kurtosis`	Calculate expanding Fisher (normalized) kurtosis time series for portfolio rate of return.
`kurtosis_rolling`([window])	Calculate rolling Fisher (normalized) kurtosis time series for portfolio rate of return.
`mean_return_annual`	Calculate annualized mean return (arithmetic mean) for the portfolio rate of return time series.
`mean_return_monthly`	Calculate monthly mean return (arithmetic mean) for the portfolio rate of return time series.
`monte_carlo_returns_ts`([distr, years, n])	Generate portfolio monthly rate of return time series with Monte Carlo simulation.
`name`	Return text name of portfolio.
`number_of_securities`	Calculate the number of securities monthly time series for the portfolio assets.
`percentile_distribution_cagr`([distr, years, ...])	Calculate percentiles for a given CAGR distribution.
`percentile_history_cagr`(years[, percentiles])	Calculate given percentiles for portfolio rolling CAGR distribution from the historical data.
`percentile_inverse_cagr`([distr, years, score, n])	Compute the percentile rank of a score (CAGR value).
`percentile_wealth`([distr, years, ...])	Calculate percentiles for portfolio wealth indexes distribution.
`percentile_wealth_history`([years, percentiles])	Calculate portfolio wealth index percentiles.
`plot_assets`([kind, tickers, pct_values, xy_text])	Plot the assets points on the risk-return chart with annotations.
`plot_forecast`([distr, years, percentiles, ...])	Plot forecasted ranges of wealth indexes (lines) for a given set of percentiles.
`plot_forecast_monte_carlo`([distr, years, n, ...])	Plot Monte Carlo simulation for portfolio wealth indexes together with historical wealth index.
`plot_hist_fit`([distr, bins])	Plot historical distribution histogram for ptrtfolio monthly rate of return time series and theoretical PDF (Probability Distribution Function).
`plot_percentiles_fit`([distr, figsize])	Generate a quantile-quantile (Q-Q) plot of portfolio monthly rate of return against quantiles of a given theoretical distribution.
`real_mean_return`	Calculate annualized real mean return (arithmetic mean) for the rate of return time series.
`rebalancing_period`	Return rebalancing period of the portfolio.
`recovery_period`	Get recovery period time series for the portfolio value.
`risk_annual`	Calculate annualized risk expanding time series for portfolio.
`risk_monthly`	Calculate monthly risk expanding time series for Portfolio.
`ror`	Calculate monthly rate of return time series for portfolio.
`semideviation_annual`	Return semideviation annualized value for portfolio rate of return time series.
`semideviation_monthly`	Calculate semi-deviation monthly value for portfolio rate of return time series.
`skewness`	Compute expanding skewness time series for portfolio rate of return.
`skewness_rolling`([window])	Compute rolling skewness of the return time series.
`symbol`	Return a text symbol of portfolio.
`symbols`	Return a list of financial symbols used to set the AssetList.
`table`	Return table with security name, ticker, weight for assets in the portfolio.
`tickers`	Return a list of tickers (symbols without a namespace) used to set the AssetList.
`wealth_index`	Calculate wealth index time series for the portfolio and accumulated inflation.
`wealth_index_with_assets`	Calculate wealth index time series for the portfolio, all assets and accumulated inflation.
`weights`	Get or set assets weights in portfolio.
`weights_ts`	Calculate assets weights time series.

property weights

Get or set assets weights in portfolio.

If not defined equal weights are used for each asset.

Weights must be a list (or tuple) of float values.

Returns:

Values for the weights of assets in portfolio.

Examples

>>> x = ok.Portfolio(['SPY.US', 'BND.US'])
>>> x.weights
[0.5, 0.5]

property weights_ts

Calculate assets weights time series.

The weights of assets in Portfolio are not constant if rebalancing_period is different from ‘month’.

Returns:

DataFrame: Weights of assets time series.

Examples

>>> import matplotlib.pyplot as plt
>>> reb_period='none'  # The Portfolio is not rebalanced.
>>> pf = ok.Portfolio(['SPY.US', 'AGG.US'], weights=[0.5, 0.5], rebalancing_period=reb_period)
>>> pf.weights_ts.plot()
>>> plt.show()

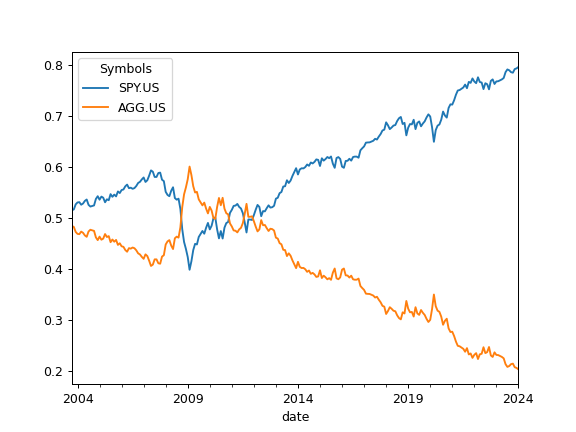
The weights of assets time series will differ significantly if the portfolio rebalancing_period is 1 year.

>>> pf.rebalancing_period = 'year'  # set a new rebalancing period
>>> pf.weights_ts.plot()
>>> plt.show()

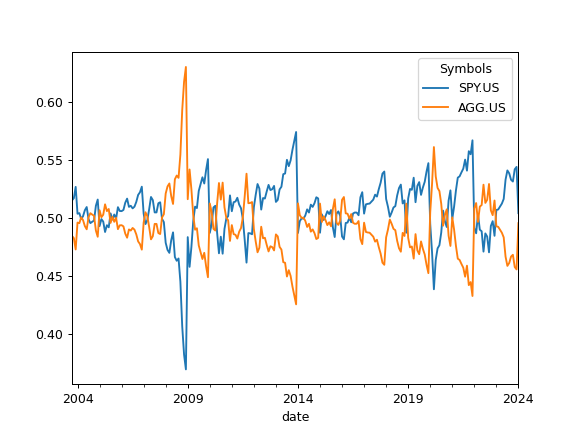
property rebalancing_period

Return rebalancing period of the portfolio.

Rebalancing is the process by which an investor restores their portfolio to its target allocation by selling and buying assets. After rebalancing all the assets have original weights.

Rebalancing period (rebalancing frequency) is predetermined time intervals when the investor rebalances the portfolio.

Returns:

str: Portfolio rebalancing period.

property symbol

Return a text symbol of portfolio.

Symbols are similar to tickers but have a namespace information:

SPY.US is a symbol
SPY is a ticker

Portfolios have ‘.PF’ as a namespace.

Returns:

str: Text symbol of the portfolio.

Examples

>>> p = ok.Portflio()
>>> p.symbol  # a randomly generated symbol will be shown
'portfolio_5312.PF'

>>> p.symbol = 'spy_portfolo.PF'  # The symbol can be customized after initialization

New Portfolio can have a custom symbol.

>>> p = ok.Portfolio(symbol='aggressive.PF')
>>> p.symbol
'aggressive.PF'

property discount_rate

Return portfolio cash flow discount rate.

Returns:

float: Cash flow discount rate.

property name

Return text name of portfolio.

For Portfolio name is equal to symbol.

Returns:

str: Text name of the portfolio.

>>> p = ok.Portfolio()
    ..

>>> p.name
    ..

‘portfolio_5312.PF’

property ror

Calculate monthly rate of return time series for portfolio.

Returns:

Series: Rate of return monthly time series for portfolio.

Examples

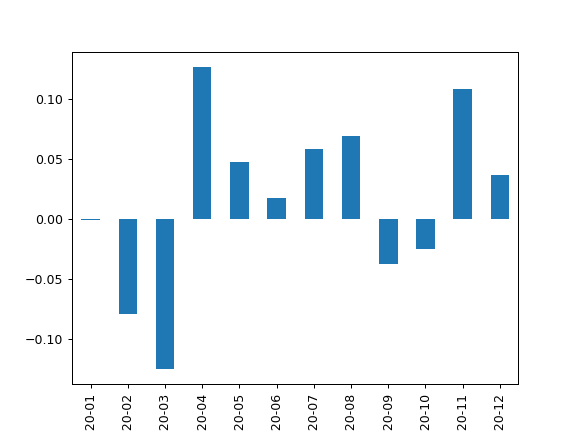
>>> pf = ok.Portfolio(first_date='2020-01', last_date='2020-12')
>>> pf.ror
Date
2020-01   -0.0004
2020-02   -0.0792
2020-03   -0.1249
2020-04    0.1270
2020-05    0.0476
2020-06    0.0177
2020-07    0.0589
2020-08    0.0698
2020-09   -0.0374
2020-10   -0.0249
2020-11    0.1088
2020-12    0.0370
Freq: M, Name: portfolio_4669.PF, dtype: float64

>>> import matplotlib.pyplot as plt
>>> pf.ror.plot(kind='bar')
>>> plt.show()

property wealth_index

Calculate wealth index time series for the portfolio and accumulated inflation.

Wealth index (Cumulative Wealth Index) is a time series that presents the value of portfolio over historical time period. Accumulated inflation time series is added if inflation=True in the Portfolio.

Wealth index is obtained from the accumulated return multiplicated by the initial investments. That is: 1000 * (Acc_Return + 1) Initial investments are taken as 1000 units of the Portfolio base currency.

Returns:

Time series of wealth index values for portfolio and accumulated inflation.

Examples

>>> import matplotlib.pyplot as plt
>>> x = ok.Portfolio(['SPY.US', 'BND.US'])
>>> x.wealth_index.plot()
>>> plt.show()

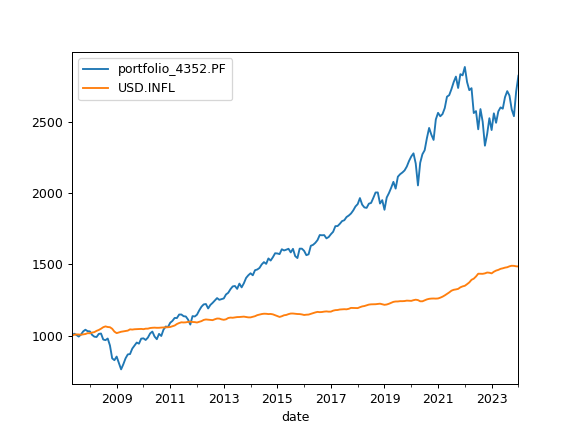
property wealth_index_with_assets

Calculate wealth index time series for the portfolio, all assets and accumulated inflation. Сash flows are not taken into account.

Wealth index (Cumulative Wealth Index) is a time series that presents the value of portfolio over historical time period. Accumulated inflation time series is added if inflation=True in the Portfolio.

Wealth index is obtained from the accumulated return multiplicated by the initial investments. initial_amount_pv * (Acc_Return + 1)

initial_amount_pv is the discounted value of the initial investments (initial_amount).

Returns:

DataFrame: Time series of wealth index values for portfolio, each asset and accumulated inflation.

Examples

>>> import matplotlib.pyplot as plt
>>> pf = ok.Portfolio(['VOO.US', 'GLD.US'], weights=[0.8, 0.2])
>>> pf.wealth_index_with_assets.plot()
>>> plt.show()

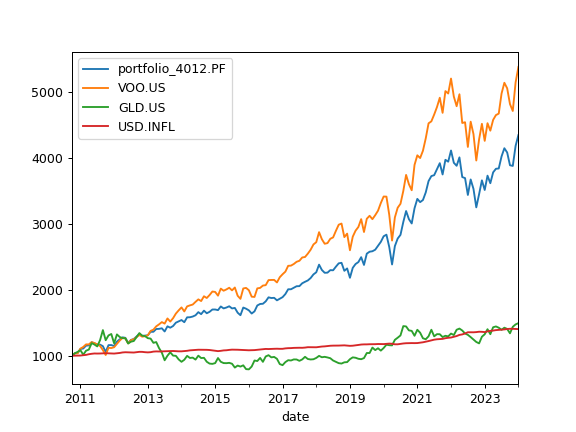
property mean_return_monthly

Calculate monthly mean return (arithmetic mean) for the portfolio rate of return time series.

Mean return calculated for the full history period.

Returns:

Float: Mean return value.

Examples

>>> pf = ok.Portfolio(['ISF.LSE', 'XGLE.LSE'], weights=[0.6, 0.4], ccy='GBP')
>>> pf
0.0001803312727272665

property mean_return_annual

Calculate annualized mean return (arithmetic mean) for the portfolio rate of return time series.

Mean return calculated for the full history period.

Returns:

Float: Mean return value.

Examples

>>> pf = ok.Portfolio(['XCS6.XETR', 'PHAU.LSE'], weights=[0.85, 0.15], ccy='USD')
>>> pf.names
{'XCS6.XETR': 'Xtrackers MSCI China UCITS ETF 1C', 'PHAU.LSE': 'WisdomTree Physical Gold'}
>>> pf.mean_return_annual
0.09005826844072184

property annual_return_ts

Calculate annual rate of return time series for portfolio.

Rate of return is calculated for each calendar year.

Returns:

DataFrame: Calendar annual rate of return time series.

Examples

>>> import matplotlib.pyplot as plt
>>> pf = ok.Portfolio(['VOO.US', 'AGG.US'], weights=[0.4, 0.6])
>>> pf.annual_return_ts.plot(kind='bar')
>>> plt.show()

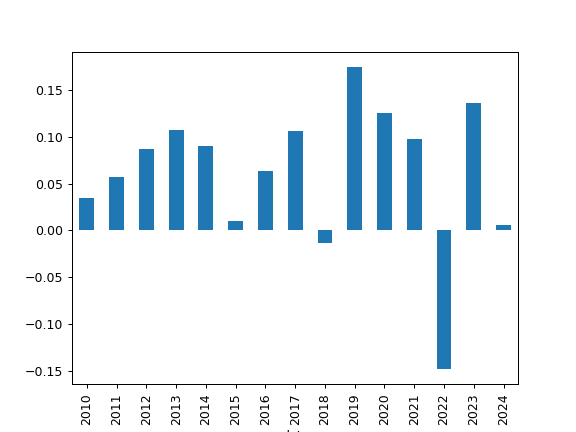
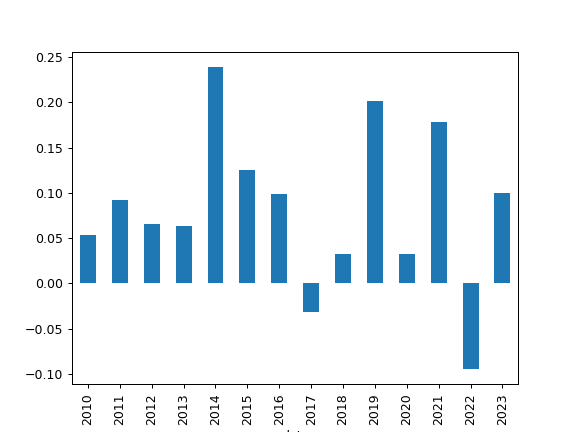
Plot annual returns for portfolio with EUR as the base currency.

>>> pf = ok.Portfolio(['VOO.US', 'AGG.US'], weights=[0.4, 0.6], ccy='EUR')
>>> pf.annual_return_ts.plot(kind='bar')
>>> plt.show()

get_cagr(period=None, real=False)

Calculate portfolio Compound Annual Growth Rate (CAGR) for a given trailing period.

Compound annual growth rate (CAGR) is the rate of return that would be required for an investment to grow from its initial to its final value, assuming all incomes were reinvested.

Inflation adjusted annualized returns (real CAGR) are shown with real=True option.

Annual inflation value is calculated for the same period if inflation=True in the AssetList.

Parameters:

period: int, optional: CAGR trailing period in years. None for the full time CAGR.
real: bool, default False: CAGR is adjusted for inflation (real CAGR) if True. Portfolio should be initiated with Inflation=True for real CAGR.

Returns:

Series: Portfolio CAGR value and annualized inflation (optional).

Notes

CAGR is not defined for periods less than 1 year (NaN values are returned).

Examples

>>> pf = ok.Portfolio(['XCS6.XETR', 'PHAU.LSE'], weights=[0.85, 0.15], ccy='USD')
>>> pf.names
{'XCS6.XETR': 'Xtrackers MSCI China UCITS ETF 1C', 'PHAU.LSE': 'WisdomTree Physical Gold'}

To get inflation adjusted return (real annualized return) add real=True option:

>>> pf.get_cagr(period=5, real=True)
portfolio_5625.PF    0.121265
dtype: float64

get_rolling_cagr(window=12, real=False)

Calculate rolling CAGR (Compound Annual Growth Rate) for the portfolio.

Parameters:

windowint, default 12: Size of the moving window in months. Window size should be at least 12 months for CAGR.
real: bool, default False: CAGR is adjusted for inflation (real CAGR) if True. Portfolio should be initiated with Inflation=True for real CAGR.

Returns:

DataFrame: Time series of rolling CAGR and mean inflation (optionaly).

Notes

CAGR is not defined for periods less than 1 year (NaN values are returned).

Examples

>>> x = ok.Portfolio(['DXET.XFRA', 'DBXN.XFRA'], ccy='EUR', inflation=True)
>>> x.get_rolling_cagr(window=5*12, real=True)
         portfolio_7645.PF
2013-09           0.029914
2013-10           0.052435
2013-11           0.055651
2013-12           0.045180
2014-01           0.063153
                    ...
2021-01           0.032734
2021-02           0.037779
2021-03           0.043811
2021-04           0.043729
2021-05           0.042704

get_cumulative_return(period=None, real=False)

Calculate cumulative return over a given trailing period for the portfolio.

The cumulative return is the total change in the portfolio price during the investment period.

Inflation adjusted cumulative returns (real cumulative returns) are shown with real=True option. Annual inflation data is calculated for the same period if inflation=True in the AssetList.

Parameters:

period: str, int or None, default None: Trailing period in years. None - full time cumulative return. ‘YTD’ - (Year To Date) period of time beginning the first day of the calendar year up to the last month.
real: bool, default False: Cumulative return is adjusted for inflation (real cumulative return) if True. Portfolio should be initiated with Inflation=True for real cumulative return.

Returns:

Series: Cumulative rate of return values for portfolio and cumulative inflation (if inflation=True in Portfolio).

Examples

>>> pf = ok.Portfolio(['BTC-USD.CC', 'LTC-USD.CC'], weights=[.8, .2], last_date='2021-03')
>>> pf.get_cumulative_return(period=2, real=True)
portfolio_6232.PF    9.39381
dtype: float64

get_rolling_cumulative_return(window=12, real=False)

Calculate rolling cumulative return.

The cumulative return is the total change in the portfolio price.

Parameters:

windowint, default 12: Size of the moving window in months.
real: bool, default False: Cumulative return is adjusted for inflation (real cumulative return) if True. Portfolio should be initiated with Inflation=True for real cumulative return.

Returns:

DataFrame: Time series of rolling cumulative return and inflation (optional).

Examples

>>> pf = ok.Portfolio(['SPY.US', 'AGG.US', 'GLD.US'], weights=[.6, .35, .05], rebalancing_period='year')
>>> pf.get_rolling_cumulative_return(window=24, real=True)
         portfolio_9012.PF
2006-11           0.125728
2006-12           0.104348
2007-01           0.129601
2007-02           0.110680
2007-03           0.132610
                    ...
2021-03           0.263755
2021-04           0.275474
2021-05           0.322736
2021-06           0.264963
2021-07           0.273801
[177 rows x 1 columns]

property assets_close_monthly

Show assets monthly close time series adjusted to the base currency.

Returns:

DataFrame: Assets monthly close time series adjusted to the base currency.

Examples

>>> import matplotlib.pyplot as plt
>>> pf = ok.Portfolio(['SPY.US', 'BND.US'], ccy='USD')
>>> pf.assets_close_monthly.plot()
>>> plt.show()

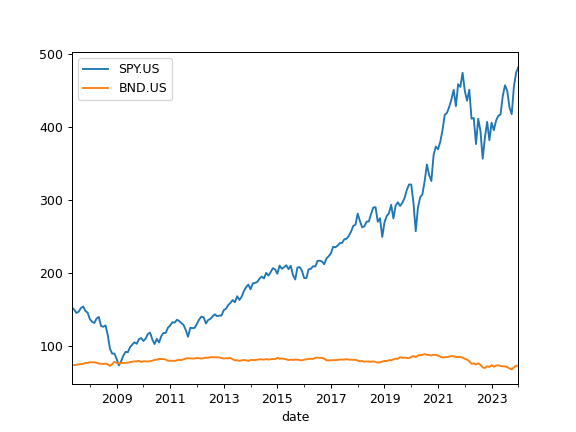
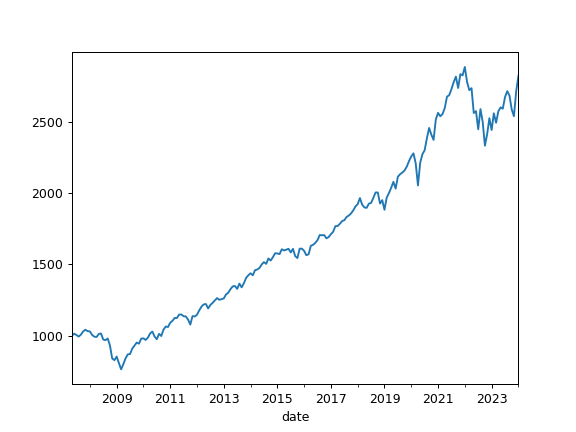
property close_monthly

Portfolio size monthly time series.

Portfolio size is shown in base currency units. It is similar to the close value of an asset. Initial portfolio value is equal to 1000 units of base currency.

Returns:

pd.Series: Monthly portfolio size time series.

Notes

‘close_mothly’ shows the same output as the ‘wealth_index’. This property is required as Portfolio must have the same attributes as an Asset.

Examples

>>> import matplotlib.pyplot as plt
>>> pf = ok.Portfolio(['SPY.US', 'BND.US'], ccy='USD')
>>> pf.close_monthly.plot()
>>> plt.show()

property number_of_securities

Calculate the number of securities monthly time series for the portfolio assets.

The number of securities in the Portfolio is changing over time as the dividends are reinvested. Portfolio rebalancing also affects the number of securities.

Initial number of securities depends on the portfolio size in base currency (1000 units).

Returns:

DataFrame: Number of securities monthly time series for the portfolio assets.

Examples

>>> pf = ok.Portfolio(['SPY.US', 'BND.US'], ccy='USD', last_date='07-2021')
>>> pf.number_of_securities
           SPY.US     BND.US
Date
2007-05  3.261153   6.687174
2007-06  3.337216   6.758447
2007-07  3.407015   6.643519
2007-08  3.410268   6.663862
2007-09  3.372630   6.798730
           ...        ...
2021-03  3.273521  15.313911
2021-04  3.204779  15.685601
2021-05  3.196768  15.749127
2021-06  3.186124  15.879056
2021-07  3.166335  16.003569
[171 rows x 2 columns]

property dividends

Calculate portfolio dividends monthly time series.

Portfolio dividends are obtained by summing asset dividends adjusted to the base currency. Dividends size depends on the portfolio value and number of securities.

Returns:

Series: Portfolio dividends monthly time series.

Examples

>>> pf = ok.Portfolio(['SPY.US', 'BND.US'], ccy='USD', last_date='07-2021')
>>> pf.dividends
2007-05    0.849271
2007-06    3.928855
2007-07    1.551262
2007-08    2.023148
2007-09    4.423416
             ...
2021-03    6.155337
2021-04    3.019478
2021-05    2.056836
2021-06    6.519521
2021-07    2.114071
Freq: M, Name: portfolio_2951.PF, Length: 171, dtype: float64

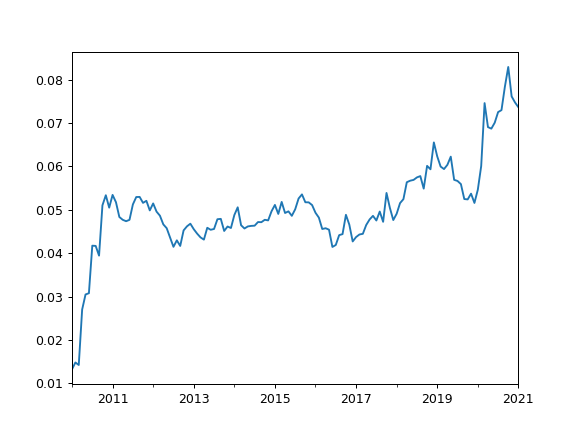
property dividend_yield

Calculate last twelve months (LTM) dividend yield time series for the portfolio. Time series has monthly values.

Portfolio dividend yield is a weighted sum of the assets dividend yields (adjusted to the portfolio base currency).

For an asset LTM dividend yield is the sum trailing twelve months of common dividends per share divided by the current price per share.

Returns:

Series: Portfolio LTM dividend yield monthly time series.

Examples

>>> pf = ok.Portfolio(['T.US', 'XOM.US'], weights=[0.8, 0.2], first_date='2010-01', last_date='2021-01', ccy='USD')
>>> pf.dividend_yield
2010-01    0.013249
2010-02    0.014835
2010-03    0.014257
             ...
2020-11    0.076132
2020-12    0.074743
2021-01    0.073643
Freq: M, Name: portfolio_8836.PF, Length: 133, dtype: float64

>>> import matplotlib.pyplot as plt
>>> pf.dividend_yield.plot()
>>> plt.show()

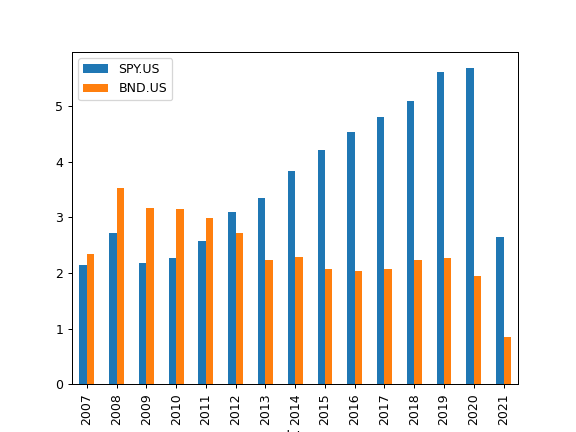
property dividends_annual

Return calendar year dividends sum time series for each asset.

Returns:

DataFrame: Annual dividends time series for each asset.

Examples

>>> import matplotlib.pyplot as plt
>>> pf = ok.Portfolio(['SPY.US', 'BND.US'], ccy='USD', last_date='07-2021')
>>> pf.dividends_annual.plot(kind='bar')
>>> plt.show()

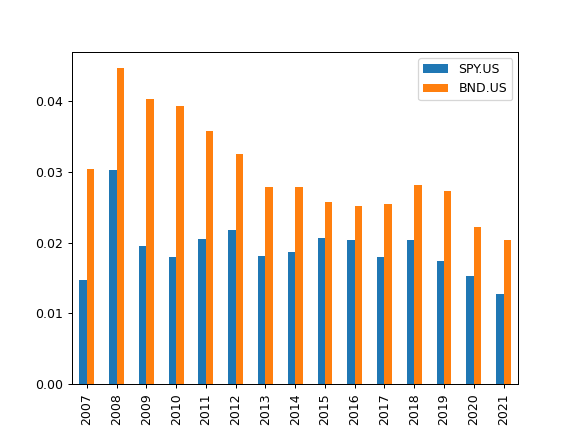
property dividend_yield_annual

Calculate last twelve months (LTM) dividend yield annual time series.

Time series is based on the dividend yield for the end of calendar year.

LTM dividend yield is the sum trailing twelve months of common dividends per share divided by the current price per share.

All yields are calculated in the asset list base currency after adjusting the dividends and price time series. Forecasted (future) dividends are removed.

Returns:

DataFrame: Time series of LTM dividend yield for each asset.

See also

dividend_yield: Dividend yield time series.
dividends_annual: Calendar year dividends time series.
dividend_paying_years: Number of years of consecutive dividend payments.
dividend_growing_years: Number of years when the annual dividend was growing.
get_dividend_mean_yield: Arithmetic mean for annual dividend yield.
get_dividend_mean_growth_rate: Geometric mean of annual dividends growth rate.

Examples

>>> import matplotlib.pyplot as plt
>>> pf = ok.Portfolio(['SPY.US', 'BND.US'], ccy='USD', last_date='07-2021')
>>> pf.dividend_yield_annual.plot(kind='bar')
>>> plt.show()

property assets_dividend_yield

Calculate last twelve months (LTM) dividend yield time series (monthly) for each asset.

LTM dividend yield is the sum trailing twelve months of common dividends per share divided by the current price per share.

All yields are calculated in the asset list base currency after adjusting the dividends and price time series. Forecasted (future) dividends are removed. Zero value time series are created for assets without dividends.

Returns:

DataFrame: Monthly time series of LTM dividend yield for each asset.

See also

dividend_yield_annual: Calendar year dividend yield time series.
dividends_annual: Calendar year dividends time series.
dividend_paying_years: Number of years of consecutive dividend payments.
dividend_growing_years: Number of years when the annual dividend was growing.
get_dividend_mean_yield: Arithmetic mean for annual dividend yield.
get_dividend_mean_growth_rate: Geometric mean of annual dividends growth rate.

Examples

>>> x = ok.AssetList(['T.US', 'XOM.US'], first_date='1984-01', last_date='1994-12')
>>> x.dividend_yield
           T.US    XOM.US
1984-01  0.000000  0.000000
1984-02  0.000000  0.002597
1984-03  0.002038  0.002589
1984-04  0.001961  0.002346
           ...       ...
1994-09  0.018165  0.012522
1994-10  0.018651  0.011451
1994-11  0.018876  0.012050
1994-12  0.019344  0.011975
[132 rows x 2 columns]

property real_mean_return

Calculate annualized real mean return (arithmetic mean) for the rate of return time series.

Real rate of return is adjusted for inflation. Real return is defined if there is an inflation=True option in Portfolio.

Returns:

float: Annualized value of the mean for the real rate of return time series.

Examples

>>> pf = ok.Portfolio(['MSFT.US', 'AAPL.US'])
>>> pf.real_mean_return
0.3088967455111862

property risk_monthly

Calculate monthly risk expanding time series for Portfolio.

Monthly risk of portfolio is a standard deviation of the rate of return time series. Standard deviation (sigma σ) is normalized by N-1.

Returns:

Series: Standard deviation of the monthly return expanding time series.

See also

risk_annual: Calculate annualized risks.
semideviation_monthly: Calculate semideviation monthly values.
semideviation_annual: Calculate semideviation annualized values.
get_var_historic: Calculate historic Value at Risk (VaR).
get_cvar_historic: Calculate historic Conditional Value at Risk (CVaR).
drawdowns: Calculate drawdowns.

Examples

>>> pf = ok.Portfolio(['MSFT.US', 'AAPL.US'])
>>> pf.risk_monthly
date
1986-05    0.020117
1986-06    0.122032
1986-07    0.130113
1986-08    0.116642
             ...
2023-08    0.092875
2023-09    0.092861
2023-10    0.092759
2023-11    0.092763
2023-12    0.092665
Freq: M, Name: portfolio_1094.PF, Length: 453, dtype: float64

property risk_annual

Calculate annualized risk expanding time series for portfolio.

Risk is a standard deviation of the rate of return.

Annualized risk is calculated for rate of retirun time series for the sample from ‘first_date’ to ‘last_date’.

Returns:

Series: Annualized standard deviation of the monthly return expanding time series.

Examples

>>> pf = ok.Portfolio(['MSFT.US', 'AAPL.US'])
>>> pf.risk_annual
date
1986-05    0.285175
1986-06    0.890909
1986-07    0.616876
1986-08    0.632270
1986-09    0.509642
             ...
2023-08    0.428297
2023-09    0.427350
2023-10    0.426961
2023-11    0.427930

property semideviation_monthly

Calculate semi-deviation monthly value for portfolio rate of return time series.

Semi-deviation (Downside risk) is the risk of the return being below the expected return.

Returns:

float: Semi-deviation monthly value for portfolio rate of return time series.

Examples

>>> pf = ok.Portfolio(['MSFT.US', 'AAPL.US'])
>>> pf.semideviation_monthly
0.05601433676604449

property semideviation_annual

Return semideviation annualized value for portfolio rate of return time series.

Semi-deviation (Downside risk) is the risk of the return being below the expected return.

Returns:

float: Annualized semi-deviation monthly value for portfolio rate of return time series.

Examples

>>> pf = ok.Portfolio(['MSFT.US', 'AAPL.US'])
>>> pf.semideviation_annual
0.1940393544621248

get_var_historic(time_frame=12, level=1)

Calculate historic Value at Risk (VaR) for the portfolio.

The VaR calculates the potential loss of an investment with a given time frame and confidence level. Loss is a positive number (expressed in cumulative return). If VaR is negative there are expected gains at this confidence level.

Parameters:

time_frameint, default 12: Time frame for VAR. Default is 12 months.
levelint, default 1: Confidence level in percents. Default value is 1%.

Returns:

Float: Historic Value at Risk (VaR) value for the portfolio.

Examples

>>> x = ok.Portfolio(['SP500TR.INDX', 'SP500BDT.INDX'], last_date='2021-01')
>>> x.get_var_historic(time_frame=12, level=1)
0.24030006476701732

get_cvar_historic(time_frame=12, level=1)

Calculate historic Conditional Value at Risk (CVAR, expected shortfall) for the portfolio.

CVaR is the average loss over a specified time period of unlikely scenarios beyond the confidence level. Loss is a positive number (expressed in cumulative return). If CVaR is negative there are expected gains at this confidence level.

Parameters:

time_frameint, default 12 (12 months): Time period size in months
levelint, default 1: Confidence level in percents to calculate the VaR. Default value is 1% (1% quantile).

Returns:

Float: Historic Conditional Value at Risk (CVAR, expected shortfall) value for the portfolio.

Examples

>>> x = ok.Portfolio(['USDEUR.FX', 'BTC-USD.CC'], last_date='2021-01')
>>> x.get_cvar_historic(time_frame=2, level=1)
0.3566909250442616

property drawdowns

Calculate drawdowns time series for the portfolio.

The drawdown is the percent decline from a previous peak in wealth index.

Returns:

Series: Drawdowns time series for the portfolio

property recovery_period

Get recovery period time series for the portfolio value.

The recovery period (drawdown duration) is the number of months to reach the value of the last maximum.

Returns:

pd.Series: Recovery period time series for the portfolio value

See also

drawdowns: Calculate drawdowns time series.

Notes

The largest recovery period does not necessary correspond to the max drawdown.

Examples

>>> pf = ok.Portfolio(['SPY.US', 'AGG.US'], weights=[0.5, 0.5])
>>> pf.recovery_period.nlargest()
date
2010-10    35
2004-10     7
2012-01     7
2019-03     6
2018-07     5
Freq: M, Name: portfolio_5724.PF, dtype: int32

describe(years=(1, 5, 10))

Generate descriptive statistics for the portfolio.

Statistics includes:

YTD (Year To date) compound return
CAGR for a given list of periods and full available period
Annualized mean rate of return (full available period)
LTM Dividend yield - last twelve months dividend yield

Risk metrics (full available period):

risk (standard deviation)
CVAR (timeframe is 1 year)
max drawdowns (and dates)

Parameters:

yearstuple of (int,), default (1, 5, 10): List of periods for CAGR statistics.

Returns:

DataFrame: Table of descriptive statistics for the portfolio.

See also

get_cumulative_return: Calculate cumulative return.
get_cagr: Calculate assets Compound Annual Growth Rate (CAGR).
dividend_yield: Calculate dividend yield (LTM).
risk_annual: Return annualized risks (standard deviation).
get_cvar: Calculate historic Conditional Value at Risk (CVAR, expected shortfall).
drawdowns: Calculate drawdowns.

Examples

>>> pf = ok.Portfolio(['SPY.US', 'BND.US'], ccy='USD', last_date='07-2021')
>>> pf.describe(years=[2, 5, 7])  # 'years' customizes the timeframe for the CAGR
            property              period portfolio_2951.PF  inflation
  compound return                 YTD          0.084098   0.048154
             CAGR             2 years          0.141465   0.031566
             CAGR             5 years          0.102494   0.025582
             CAGR             7 years          0.091694   0.019656
             CAGR  14 years, 3 months          0.074305   0.019724
   Dividend yield                 LTM          0.016504        NaN
             Risk  14 years, 3 months          0.086103        NaN
             CVAR  14 years, 3 months          0.214207        NaN
     Max drawdown  14 years, 3 months         -0.266915        NaN
Max drawdown date  14 years, 3 months           2009-02        NaN

property table

Return table with security name, ticker, weight for assets in the portfolio.

Returns:

DataFrame: Security name - ticker - weight table.

Examples

>>> pf = ok.Portfolio(["MSFT.US", "AAPL.US"])
>>> pf.table
                asset name   ticker  weights
0  Microsoft Corporation  MSFT.US      0.5
1              Apple Inc  AAPL.US      0.5

percentile_inverse_cagr(distr='norm', years=1, score=0, n=None)

Compute the percentile rank of a score (CAGR value).

Percentile rank can be calculated for given distribution type or for hsitorical distribution of CAGR.

If percentile_inverse of, for example, 0% (CAGR value) is equal to 8% for 1 year time frame it means that 8% of the CAGR values in the distribution are negative in 1 year periods. Or in other words the probability of getting negative result after 1 year of investments is 8%.

Parameters:

distr: {‘norm’, ‘lognorm’, ‘hist’}, default ‘norm’: The rate of teturn distribution type. ‘norm’ - for normal distribution. ‘lognorm’ - for lognormal distribution. ‘hist’ - percentiles are taken from the historical data.
years: int, default 1: Period length (time frame) in years when CAGR is calculated.
score: float, default 0: Score that is compared to the elements in CAGR array.
n: int, optional: Number of random time series with the defined distributions (for ‘norm’ or ‘lognorm’ only). Larger argument values can be used to increase the precision of the calculation. But this will lead to slower performance. Is not required for historical distribution (dist=’hist’). For ‘norm’ or ‘lognorm’ distribution default value n=1000 is used.

Returns:

float: Percentile-position of score (0-100) relative to distribution.

Examples

>>> pf = ok.Portfolio(['SPY.US', 'AGG.US', 'GLD.US'], weights=[.60, .35, .05], rebalancing_period='year')
>>> pf.percentile_inverse_cagr(distr='lognorm', score=0, years=1, n=5000)
18.08
The probability of getting negative result (score=0) in 1 year period for lognormal distribution.

percentile_history_cagr(years, percentiles=[10, 50, 90])

Calculate given percentiles for portfolio rolling CAGR distribution from the historical data.

CAGR - Compound Annual Growth Rate. Each percentile is calculated for a period range from 1 year to ‘years’.

Parameters:

years: int, default 1: Max window size for rolling CAGR in the distribution in years. It should not exceed 1/2 of the portfolio history period length ‘period_length’.
percentiles: list of int, default [10, 50, 90]: List of percentiles to be calculated.

Returns:

DataFrame: Table with percentiles values for each period from 1 to ‘years’.

Examples

>>> pf = ok.Portfolio(['SPY.US', 'AGG.US', 'GLD.US'], weights=[.60, .35, .05], rebalancing_period='none')
>>> pf.percentile_history_cagr(years=5, percentiles=[1, 50, 99])
             1         50        99
years
1     -0.231327  0.098693  0.295343
2     -0.101689  0.091824  0.206471
3     -0.036771  0.085428  0.157833
4     -0.007674  0.085178  0.142195
5      0.030933  0.082865  0.134496

percentile_wealth_history(years=1, percentiles=[10, 50, 90])

Calculate portfolio wealth index percentiles.

Percentiles are derived from rolling CAGR historical distribution. CAGR - Compound Annual Growth Rate. Wealth index (Cumulative Wealth Index) is a time series that presents the value of portfolio over a given time period.

Actual portfolio wealth is adjusted to the last known historical value (from ‘wealth_index’). It is useful for a chart with historical wealth index and forecasted values.

Parameters:

years: int, default 1: Time frame for portfolio wealth index percentiles. It should not exceed 1/2 of the portfolio history period length ‘period_length’. Percentiles are calculated for periods from 1 to ‘years’.
percentiles: list of int, default [10, 50, 90]: List of percentiles to be calculated.

Returns:

DataFrame: Table with portfolio wealth index percentiles for each period from 1 to ‘years’.

Examples

>>> pf = ok.Portfolio(['SPY.US', 'AGG.US', 'GLD.US'], weights=[.60, .35, .05], rebalancing_period='month')
>>> pf.percentile_wealth_history(years=5)
                10           50           90
years
1      3815.660408  4202.758919  4457.210561
2      3727.946026  4540.888480  5005.291952
3      3797.214674  4855.631902  5384.216628
4      4173.503054  5274.584657  6018.571025
5      4613.287195  5706.343210  6694.576137

monte_carlo_returns_ts(distr='norm', years=1, n=100)

Generate portfolio monthly rate of return time series with Monte Carlo simulation.

Monte Carlo simulation generates n random monthly time series with a given distribution. Forecast period should not exceed 1/2 of portfolio history period length.

First date of forecaseted returns is portfolio last_date.

Parameters:

distr{‘norm’, ‘lognorm’}, default ‘norm’: Distribution type for rate of return time series. ‘norm’ - for normal distribution. ‘lognorm’ - for lognormal distribution.
yearsint, default 1: Forecast period for portfolio monthly rate of return time series. It should not exceed 1/2 of the portfolio history period length ‘period_length’.
nint, default 100: Number of random rate of return time series to generate with Monte Carlo simulation.

Returns:

DataFrame: Table with n random rate of return monthly time series.

Examples

>>> pf = ok.Portfolio(['SPY.US', 'AGG.US', 'GLD.US'], weights=[.60, .35, .05], rebalancing_period='month')
>>> pf.monte_carlo_returns_ts(years=8, distr='norm', n=5000)
             0         1         2     ...      4997      4998      4999
2021-07 -0.008383 -0.013167 -0.031659  ...  0.046717  0.065675  0.017933
2021-08  0.038773 -0.023627  0.039208  ... -0.016075  0.034439  0.001856
2021-09  0.005026 -0.007195 -0.003300  ... -0.041591  0.021173  0.114225
2021-10 -0.007257  0.003013 -0.004958  ...  0.037057 -0.009689 -0.003242
2021-11 -0.005006  0.007090  0.020741  ...  0.026509 -0.023554  0.010271
           ...       ...       ...  ...       ...       ...       ...
2029-02 -0.065898 -0.003673  0.001198  ...  0.039293  0.015963 -0.050704
2029-03  0.021215  0.008783 -0.017003  ...  0.035144  0.002169  0.015055
2029-04  0.002454 -0.016281  0.017004  ...  0.032535  0.027196 -0.029475
2029-05  0.011206  0.023396 -0.013757  ... -0.044717 -0.025613 -0.002066
2029-06 -0.016740 -0.007955  0.002862  ... -0.027956 -0.012339  0.048974
[96 rows x 5000 columns]

percentile_distribution_cagr(distr='norm', years=1, percentiles=[10, 50, 90], n=10000)

Calculate percentiles for a given CAGR distribution.

CAGR - Compound Annual Growth Rate. CAGR is calculated for each of n random returns time series of a given distribution. Random time series are generated with Monte Carlo simulation. CAGR time frame should not exceed 1/2 of portfolio history period length.

Parameters:

distr{‘norm’, ‘lognorm’}, default ‘norm’: Distribution type for the rate of return of portfolio. ‘norm’ - for normal distribution. ‘lognorm’ - for lognormal distribution.
years: int, default 1: Time frame for portfolio CAGR. It should not exceed 1/2 of the portfolio history period length ‘period_length’.
percentiles: list of int, default [10, 50, 90]: List of percentiles to be calculated.
nint, default 10000: Number of random time series to generate with Monte Carlo simulation. Larger argument values can be used to increase the precision of the calculation. But this will lead to slower performance.

Returns:

dict: Dictionary {Percentile: value}

Examples

>>> pf = ok.Portfolio(['SPY.US', 'AGG.US', 'GLD.US'], weights=[.60, .35, .05], rebalancing_period='year')
>>> pf.percentile_distribution_cagr()
{10: -0.0329600265453808, 50: 0.08247141141668779, 90: 0.21338327078214836}
Forecast CAGR according to normal distribution within 1 year period.
>>> pf.percentile_distribution_cagr(years=5)
{10: 0.030625112922274055, 50: 0.08346815557550402, 90: 0.13902575176654647}
Forecast CAGR according to normal distribution within 5 year period.

percentile_wealth(distr='norm', years=1, percentiles=[10, 50, 90], today_value=None, n=1000)

Calculate percentiles for portfolio wealth indexes distribution.

Portfolio wealth indexes are derived from the rate of return time series of a given distribution type.

Parameters:

distr{‘hist’, ‘norm’, ‘lognorm’}, default ‘norm’: Distribution type for the rate of return of portfolio. ‘norm’ - for normal distribution. ‘lognorm’ - for lognormal distribution. ‘hist’ - percentiles are taken from the historical data.
yearsint, default 1: Investment period length to calculate wealth index. It should not exceed 1/2 of the portfolio history period length ‘period_length’.
percentileslist of int, default [10, 50, 90]: List of percentiles to be calculated.
today_valueint, optional: Initial value of the wealth index. If today_value is None the last value of the historical wealth indexes is taken. It can be useful to plot the forecast of wealth index togeather with the hitorical data.
nint, default 1000: Number of random time series to generate with Monte Carlo simulation (for ‘norm’ or ‘lognorm’ only). Larger argument values can be used to increase the precision of the calculation. But this will lead to slower performance. Is not required for historical distribution (dist=’hist’).

Returns:

dict: Dictionary {Percentile: value}

Examples

>>> pf = ok.Portfolio(['SPY.US', 'AGG.US', 'GLD.US'], weights=[.60, .35, .05], rebalancing_period='year')
>>> pf.percentile_wealth(distr='hist', years=5, today_value=1000, n=5000)
{10: 1228.3741255659957, 50: 1491.7857161011104, 90: 1745.1130920663286}
Percentiles values for the wealth index 5 years forecast if the initial value is 1000.

property skewness

Compute expanding skewness time series for portfolio rate of return.

For normally distributed data, the skewness should be about zero. A skewness value greater than zero means that there is more weight in the right tail of the distribution.

Returns:

Series: Expanding skewness time series

Examples

>>> pf = ok.Portfolio(['BND.US'])
>>> pf.skewness
Date
2008-05   -0.134193
2008-06   -0.022349
2008-07    0.081412
2008-08   -0.020978
             ...
2021-04    0.441430
2021-05    0.445772
2021-06    0.437383
2021-07    0.425247
Freq: M, Name: portfolio_8378.PF, Length: 159, dtype: float64

>>> import matplotlib.pyplot as plt
>>> pf.skewness.plot()
>>> plt.show()

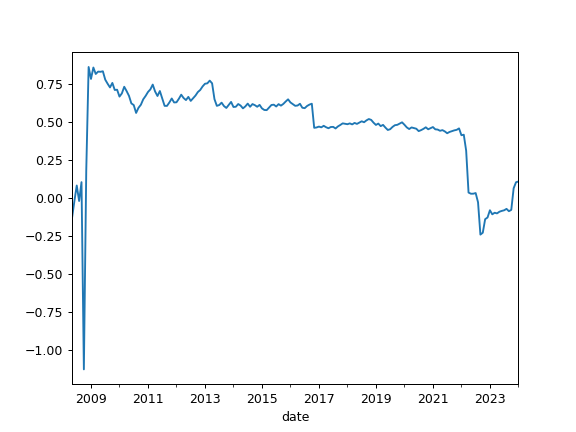
skewness_rolling(window=60)

Compute rolling skewness of the return time series.

For normally distributed rate of return, the skewness should be about zero. A skewness value greater than zero means that there is more weight in the right tail of the distribution.

Parameters:

windowint, default 60: Size of the moving window in months. The window size should be at least 12 months.

Returns:

Series: Expanding skewness time series

Examples

>>> pf = ok.Portfolio(['BND.US'])
>>> pf.skewness_rolling(window=12*10)
Date
2017-04    0.464916
2017-05    0.446095
2017-06    0.441211
2017-07    0.453947
2017-08    0.464805
...
2021-02    0.007622
2021-03    0.000775
2021-04    0.002308
2021-05    0.022543
2021-06   -0.006534
2021-07   -0.012192
Freq: M, Name: portfolio_8378.PF, dtype: float64

>>> import matplotlib.pyplot as plt
>>> pf.skewness_rolling(window=12*10).plot()
>>> plt.show()

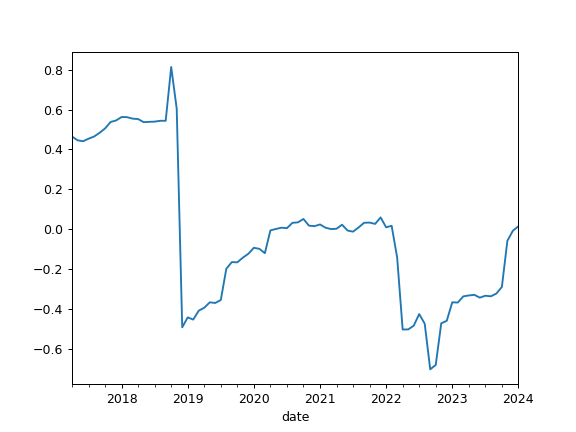
property kurtosis

Calculate expanding Fisher (normalized) kurtosis time series for portfolio rate of return.

Kurtosis is a measure of whether the rate of return are heavy-tailed or light-tailed relative to a normal distribution. It should be close to zero for normally distributed rate of return. Kurtosis is the fourth central moment divided by the square of the variance.

Returns:

Series: Expanding kurtosis time series

Examples

>>> pf = ok.Portfolio(['BND.US'])
>>> pf.kurtosis
Date
2008-05   -0.815206
2008-06   -0.718330
2008-07   -0.610741
2008-08   -0.534105
             ...
2021-04    2.821322
2021-05    2.855267
2021-06    2.864717
2021-07    2.850407
Freq: M, Name: portfolio_4411.PF, Length: 159, dtype: float64

>>> import matplotlib.pyplot as plt
>>> pf.kurtosis.plot()
>>> plt.show()

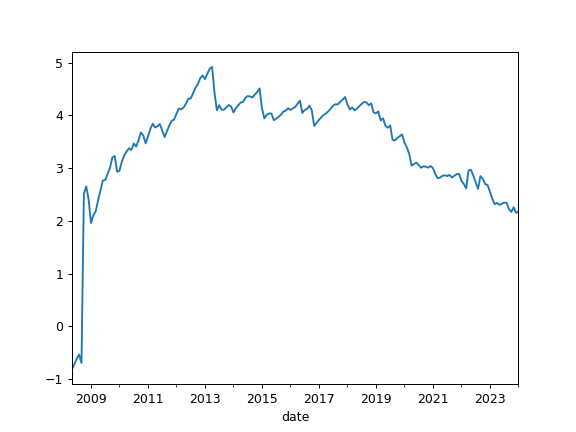
kurtosis_rolling(window=60)

Calculate rolling Fisher (normalized) kurtosis time series for portfolio rate of return.

Kurtosis is a measure of whether the rate of return are heavy-tailed or light-tailed relative to a normal distribution. It should be close to zero for normally distributed rate of return. Kurtosis is the fourth central moment divided by the square of the variance.

Parameters:

windowint, default 60: Size of the moving window in months. The window size should be at least 12 months.

Returns:

Series: Expanding kurtosis time series.

Examples

>>> pf = ok.Portfolio(['BND.US'])
>>> pf.kurtosis_rolling(window=12*10)
Date
2017-04    4.041599
2017-05    4.133518
2017-06    4.165099
2017-07    4.205125
2017-08    4.313773
...
2021-03    0.362184
2021-04    0.409680
2021-05    0.455760
2021-06    0.457315
2021-07    0.496168
Freq: M, Name: portfolio_4411.PF, dtype: float64

>>> import matplotlib.pyplot as plt
>>> pf.kurtosis_rolling(window=12*10).plot()
>>> plt.show()

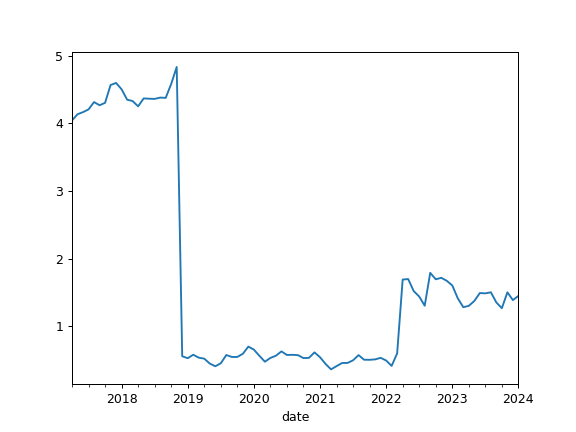
property jarque_bera

Perform Jarque-Bera test for normality of portfolio returns time series.

Jarque-Bera shows whether the returns have the skewness and kurtosis matching a normal distribution (null hypothesis or H0).

Returns:

dict: Jarque-Bera test statistics and p-value.

Notes

Test returns statistics (first row) and p-value (second row). p-value is the probability of obtaining test results, under the assumption that the null hypothesis is correct. In general, a large Jarque-Bera statistics and tiny p-value indicate that null hypothesis is rejected and the time series are not normally distributed.

Examples

>>> pf = ok.Portfolio(['BND.US'])
>>> pf.jarque_bera
{'statistic': 58.27670538027455, 'p-value': 2.2148949341271873e-13}

kstest(distr='norm')

Perform one sample Kolmogorov-Smirnov test on portfolio returns and evaluate goodness of fit for a given distribution.

The one-sample Kolmogorov-Smirnov test compares the rate of return time series against a given distribution.

Parameters:

distr{‘norm’, ‘lognorm’}, default ‘norm’: The name of a distribution to fit. ‘norm’ - for normal distribution. ‘lognorm’ - for lognormal distribution.

Returns:

dict: Kolmogorov-Smirnov test statistics and p-value.

Notes

Like in Jarque-Bera test returns statistic (first row) and p-value (second row). Null hypotesis (two distributions are similar) is not rejected when p-value is high enough. 5% threshold can be used.

Examples

>>> pf = ok.Portfolio(['GLD.US'])
>>> pf.kstest(distr='lognorm')
{'statistic': 0.05001344986084533, 'p-value': 0.6799422889377373}

>>> pf.kstest(distr='norm')
{'statistic': 0.09528000069992831, 'p-value': 0.047761781235967415}

Kolmogorov-Smirnov test shows that GLD rate of return time series fits lognormal distribution better than normal one.

get_sharpe_ratio(rf_return=0)

Calculate Sharpe ratio.

The Sharpe ratio is the average annual return in excess of the risk-free rate per unit of risk (annualized standard deviation).

Risk-free rate should be taken according to the Portfolio base currency.

Parameters:

rf_returnfloat, default 0: Risk-free rate of return.

Returns:

float

Examples

>>> pf = ok.Portfolio(['VOO.US', 'BND.US'], weights=[0.40, 0.60])
>>> pf.get_sharpe_ratio(rf_return=0.04)
0.7412193684695373

get_sortino_ratio(t_return=0)

Calculate Sortino ratio for the portfolio with specified target return.

Sortion ratio measures the risk-adjusted return of portfolio. It is a modification of the Sharpe ratio but penalizes only those returns falling below a specified target rate of return, while the Sharpe ratio penalizes both upside and downside volatility equally.

Parameters:

t_returnfloat, default 0: Traget rate of return.

Returns:

float

Examples

>>> pf = ok.Portfolio(['VOO.US', 'BND.US'], last_date='2021-12')
>>> pf.get_sortino_ratio(t_return=0.02)
1.4377728903230174

property diversification_ratio

Calculate Diversification Ratio for the portfolio.

The Diversification Ratio is the ratio of the weighted average of assets risks divided by the portfolio risk. In this case risk is the annuilized standatd deviation for the rate of return .

Returns:

float

Examples

>>> pf = ok.Portfolio(['VOO.US', 'BND.US'], weights=[0.7, 0.3], last_date='2021-12')
>>> pf.diversification_ratio
1.1264305597257505

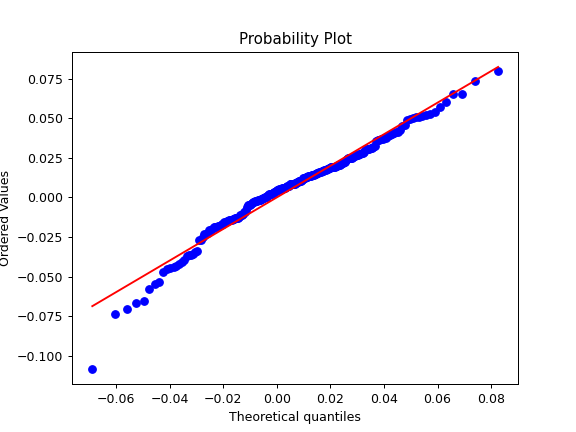
plot_percentiles_fit(distr='norm', figsize=None)

Generate a quantile-quantile (Q-Q) plot of portfolio monthly rate of return against quantiles of a given theoretical distribution.

A q-q plot is a plot of the quantiles of the portfolio rate of return historical data against the quantiles of a given theoretical distribution.

Parameters:

distr{‘norm’, ‘lognorm’}, default ‘norm’: The name of a distribution to fit. ‘norm’ - for normal distribution. ‘lognorm’ - for lognormal distribution.
figsize(float, float), optional: Width and height of plot in inches. If None default matplotlib figsize value is used.

Examples

>>> import matplotlib.pyplot as plt
>>> pf = ok.Portfolio(['SPY.US', 'AGG.US', 'GLD.US'], weights=[.60, .35, .05], rebalancing_period='year')
>>> pf.plot_percentiles_fit(distr='lognorm')
>>> plt.show()

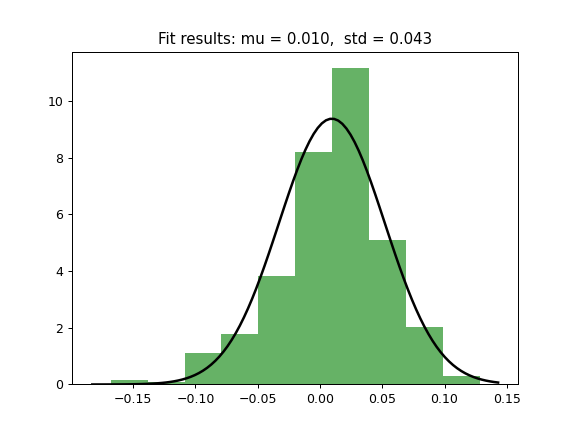
plot_hist_fit(distr='norm', bins=None)

Plot historical distribution histogram for ptrtfolio monthly rate of return time series and theoretical PDF (Probability Distribution Function).

Examples

>>> import matplotlib.pyplot as plt
>>> pf = ok.Portfolio(['SP500TR.INDX'])
>>> pf.plot_hist_fit(distr='norm')
>>> plt.show()

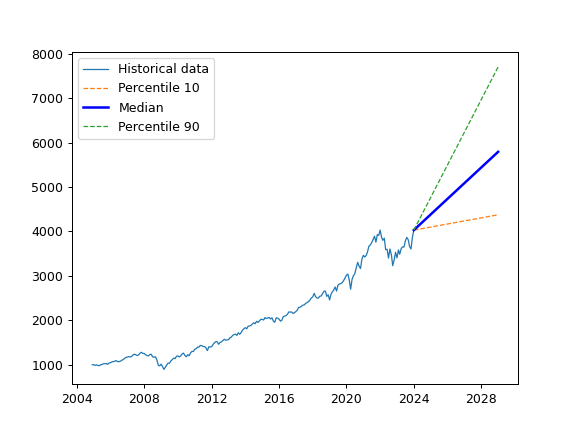
plot_forecast(distr='norm', years=5, percentiles=[10, 50, 90], today_value=None, n=1000, figsize=None)

Plot forecasted ranges of wealth indexes (lines) for a given set of percentiles. Historical wealth index is shown in the same chart.

Parameters:

distr{‘hist’, ‘norm’, ‘lognorm’}, default ‘norm’: Distribution type for the rate of return of portfolio. ‘norm’ - for normal distribution. ‘lognorm’ - for lognormal distribution. ‘hist’ - percentiles are taken from the historical data.
yearsint, default 1: Investment period length to calculate wealth index. It should not exceed 1/2 of the portfolio history period length ‘period_length’.
percentileslist of int, default [10, 50, 90]: List of percentiles to be calculated.
today_valueint, optional: Initial value of the wealth index. If today_value is None the last value of the historical wealth indexes is taken. It can be useful to plot the forecast of wealth index togeather with the hitorical data.
nint, default 1000: Number of random time series to generate with Monte Carlo simulation (for ‘norm’ or ‘lognorm’ only). Larger argument values can be used to increase the precision of the calculation. But this will lead to slower performance. Is not required for historical distribution (dist=’hist’).

Returns:

Axes‘matplotlib.axes._subplots.AxesSubplot’

Examples

>>> import matplotlib.pyplot as plt
>>> pf = ok.Portfolio(['SPY.US', 'AGG.US', 'GLD.US'], weights=[.60, .35, .05], rebalancing_period='year')
>>> pf.plot_forecast()
>>> plt.show()

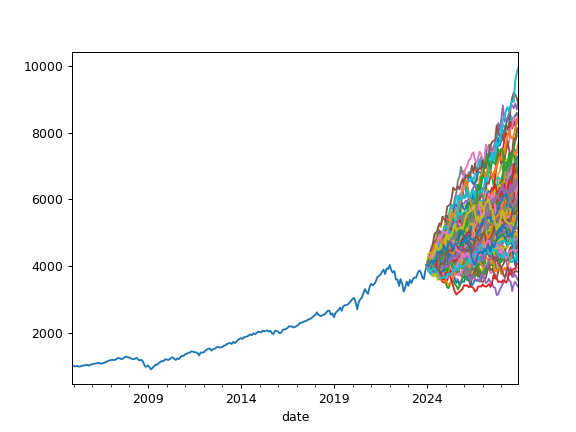
plot_forecast_monte_carlo(distr='norm', years=1, n=20, figsize=None)

Plot Monte Carlo simulation for portfolio wealth indexes together with historical wealth index.

Random wealth indexes are generated according to a given distribution.

Parameters:

distr{‘norm’, ‘lognorm’}, default ‘norm’: Distribution type for the rate of return of portfolio. ‘norm’ - for normal distribution. ‘lognorm’ - for lognormal distribution.
yearsint, default 1: Investment period length for new wealth indexes It should not exceed 1/2 of the portfolio history period length ‘period_length’.
nint, default 20: Number of random wealth indexes to generate with Monte Carlo simulation.
figsize(float, float), optional: Width, height in inches. If None default matplotlib figsize value is used.

Examples

>>> import matplotlib.pyplot as plt
>>> pf = ok.Portfolio(['SPY.US', 'AGG.US', 'GLD.US'],
...                    weights=[.60, .35, .05],
...                    rebalancing_period='year')
>>> pf.plot_forecast_monte_carlo(years=5, distr='lognorm', n=100)
>>> plt.show()

property currency

Return the base currency of the Asset List.

Such properties as rate of return and risk are adjusted to the base currency.

Returns:

okama.Asset: Base currency of the Asset List in form of okama.Asset class.

plot_assets(kind='mean', tickers='tickers', pct_values=False, xy_text=(0, 10))

Plot the assets points on the risk-return chart with annotations.

Annualized values for risk and return are used. Risk is a standard deviation of monthly rate of return time series. Return can be an annualized mean return (expected return) or CAGR (Compound annual growth rate).

Parameters:

kind{‘mean’, ‘cagr’}, default ‘mean’: Type of Return: annualized mean return (expected return) or CAGR (Compound annual growth rate).
tickers{‘tickers’, ‘names’} or list of str, default ‘tickers’: Annotation type for assets. ‘tickers’ - assets symbols are shown in form of ‘SPY.US’ ‘names’ - assets names are used like - ‘SPDR S&P 500 ETF Trust’ To show custom annotations for each asset pass the list of names.
pct_valuesbool, default False: Risk and return values in the axes: Algebraic annotation (False) Percents (True)
xy_texttuple, default (0, 10): The shift of the annotation text (x, y) from the point.

Returns:

Axes‘matplotlib.axes._subplots.AxesSubplot’

Examples

>>> import matplotlib.pyplot as plt
>>> al = ok.AssetList(['SPY.US', 'AGG.US'], ccy='USD', inflation=False)
>>> al.plot_assets()
>>> plt.show()

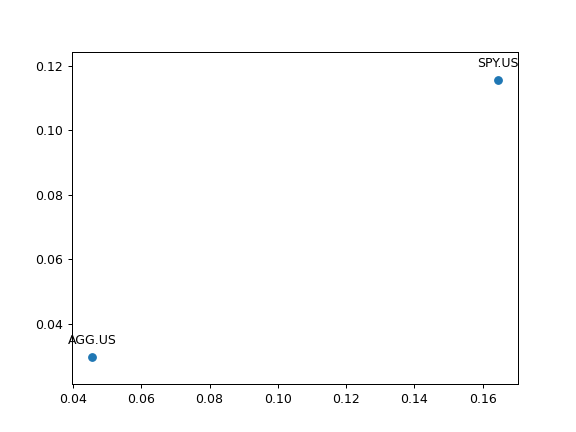
Plotting with default parameters values shows expected return, ticker annotations and algebraic values for risk and return. To use CAGR instead of expected return use kind=’cagr’.

>>> al.plot_assets(kind='cagr',
...               tickers=['US Stocks', 'US Bonds'],  # use custom annotations for the assets
...               pct_values=True  # risk and return values are in percents
...               )
>>> plt.show()

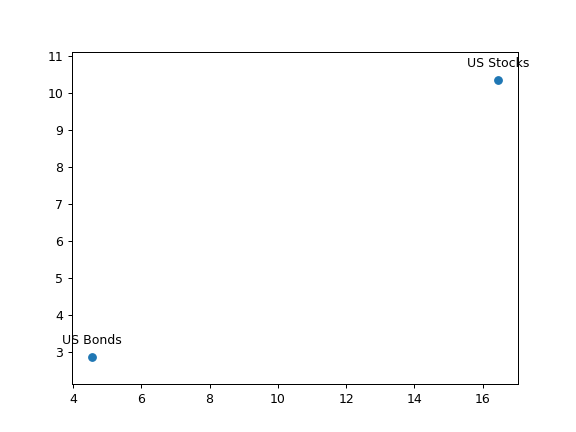
property symbols

Return a list of financial symbols used to set the AssetList.

Symbols are similar to tickers but have a namespace information:

SPY.US is a symbol
SPY is a ticker

Returns:

list of str: List of symbols included in the Asset List.

property tickers

Return a list of tickers (symbols without a namespace) used to set the AssetList.

tickers are similar to symbols but do not have namespace information:

SPY is a ticker
SPY.US is a symbol

Returns:

list of str: List of tickers included in the Asset List.