okama.EfficientFrontier

class EfficientFrontier(assets=None, *, first_date=None, last_date=None, ccy='USD', bounds=None, inflation=False, full_frontier=True, n_points=20, ticker_names=True)

Bases: AssetList

Efficient Frontier with classic Mean-Variance optimization.

Efficient Frontier is a set of portfolios which satisfy the condition that no other portfolio exists with a higher expected return but with the same risk (standard deviation of return).

The points on the Efficient Frontier are obtained through the constrained optimization process (optimization with bounds). Bounds are defined with ‘bounds’ property.

In classic Markowitz optimization portfolios are rebalanced monthly and has constant weights (single period optimization).

Parameters:

assetslist, default None: List of assets. Could include tickers or asset like objects (Asset, Portfolio). If None a single asset list with a default ticker is used.
first_datestr, default None: First date of monthly return time series. If None the first date is calculated automatically as the oldest available date for the listed assets.
last_datestr, default None: Last date of monthly return time series. If None the last date is calculated automatically as the newest available date for the listed assets.
ccystr, default ‘USD’: Base currency for the list of assets. All risk metrics and returns are adjusted to the base currency.
bounds: tuple of ((float, float),…): Bounds for the assets weights. Each asset can have weights limitation from 0 to 1.0. If an asset has limitation for 10 to 20%, bounds are defined as (0.1, 0.2). bounds = ((0, .5), (0, 1)) shows that in Portfolio with two assets first one has weight limitations from 0 to 50%. The second asset has no limitations.
inflationbool, default True: Defines whether to take inflation data into account in the calculations. Including inflation could limit available data (last_date, first_date) as the inflation data is usually published with a one-month delay. With inflation = False some properties like real return are not available.
n_pointsint, default 20: Number of points in the Efficient Frontier.
full_frontierbool, default True: Defines whether to show the full Efficient Frontier or only its upper part. If ‘False’ Efficient Frontier has only the points with the return above Global Minimum Volatility (GMV) point.
ticker_namesbool, default True: Defines whether to include full names of assets in the optimization report or only tickers.

Methods & Attributes

`bounds`	Return bounds for the assets weights.
`ef_points`	Generate single period Efficient Frontier.
`get_assets_tickers`()
`get_monte_carlo`([n, kind])	Generate N random portfolios with Monte Carlo simulation.
`get_most_diversified_portfolio`([...])	Calculate assets weights, risk, return and Diversification ratio for the most diversified portfolio given the target return within given bounds.
`get_tangency_portfolio`([rf_return, ...])	Calculate asset weights, risk and return values for tangency portfolio within given bounds.
`gmv_annualized`	Calculate the annualized risk and return of the Global Minimum Volatility (GMV) portfolio within given bounds.
`gmv_monthly`	Calculate the monthly risk and return of the Global Minimum Volatility (GMV) portfolio within given bounds.
`gmv_weights`	Calculate asset weights of the Global Minimum Volatility (GMV) portfolio within given bounds.
`mdp_points`	Generate Most diversified portfolios line.
`mean_return_range`	Calculate the range of mean monthly returns (from min to max).
`minimize_risk`(target_return[, ...])	Find minimal risk given the target return within given bounds.
`optimize_return`([option])	Find a portfolio with global max or min for the rate of return within given bounds.
`plot_cml`([rf_return, y_axe, figsize])	Plot Capital Market Line (CML).
`plot_pair_ef`([tickers, figsize])	Plot Efficient Frontier of every pair of assets.
`plot_transition_map`([x_axe, figsize])	Plot Transition Map for optimized portfolios on the single period Efficient Frontier.

property bounds

Return bounds for the assets weights.

Bounds are used in Mean-Variance optimization. Each asset can have weights limitation from 0 to 1.0.

If an asset has limitation for 10 to 20% bounds are defined as (0.1, 0.2). bounds = ((0, .5), (0, 1)) shows that in Portfolio with two assets first one has weight limitations from 0 to 50%. The second asset has no limitations.

Returns:

tuple of ((float, float),…): Weights bounds used for portfolio optimization.

Examples

>>> two_assets = ok.EfficientFrontier(['SPY.US', 'AGG.US'])
>>> two_assets.bounds
((0.0, 1.0), (0.0, 1.0))

By default there are no limitations for assets weights. Bounds can be set for a Efficient Frontier object.

>>> two_assets.bounds = ((0.5, 0.9), (0, 1.0))

Now the optimization is bounded (SPY has weights limits from 50 to 90%).

property gmv_weights

Calculate asset weights of the Global Minimum Volatility (GMV) portfolio within given bounds.

Global Minimum Volatility portfolio is a portfolio with the lowest risk of all possible. Along the Efficient Frontier, the left-most point is a portfolio with minimum risk when compared to all possible portfolios of risky assets.

In Mean-Variance optimization risk is defined as a standard deviation of return time series.

Bounds are defined with ‘bounds’ property.

Returns:

numpy.ndarray: GMV portfolio assets weights.

Examples

>>> two_assets = ok.EfficientFrontier(['SPY.US', 'AGG.US'])
>>> two_assets.gmv_weights
array([0.05474178, 0.94525822])

property gmv_monthly

Calculate the monthly risk and return of the Global Minimum Volatility (GMV) portfolio within given bounds.

Global Minimum Volatility portfolio is a portfolio with the lowest risk of all possible. Along the Efficient Frontier, the left-most point is a portfolio with minimum risk when compared to all possible portfolios of risky assets.

In Mean-Variance optimization risk is defined as a standard deviation of return time series.

Bounds are defined with ‘bounds’ property.

Returns:

tuple: risk, return monthly values for GMV portfolio.

Examples

>>> ef = ok.EfficientFrontier(['SPY.US', 'AGG.US', 'GLD.US'])
>>> ef.gmv_monthly
(0.01024946425526032, 0.0036740056018316597)

property gmv_annualized

Calculate the annualized risk and return of the Global Minimum Volatility (GMV) portfolio within given bounds.

Global Minimum Volatility portfolio is a portfolio with the lowest risk of all possible. Along the Efficient Frontier, the left-most point is a portfolio with minimum risk when compared to all possible portfolios of risky assets.

In Mean-Variance optimization risk is defined as a standard deviation of return time series.

Bounds are defined with ‘bounds’ property.

Returns:

tuple: risk, return annualized values for GMV portfolio.

Examples

>>> ef = ok.EfficientFrontier(['SPY.US', 'AGG.US', 'GLD.US'])
>>> ef.gmv_annualized
(0.03697734994430258, 0.0449899573148429)

get_tangency_portfolio(rf_return=0, rate_of_return='cagr')

Calculate asset weights, risk and return values for tangency portfolio within given bounds.

Tangency portfolio or Maximum Sharpe Ratio (MSR) is the point on the Efficient Frontier where Sharpe Ratio reaches its maximum.

The Sharpe ratio is the average annual return in excess of the risk-free rate per unit of risk (annualized standard deviation).

Bounds are defined with ‘bounds’ property.

Parameters:

rate_of_return{cagr, mean_return}, default cagr: Use CAGR (Compound annual growth rate) or arithmetic mean of return to calculate Sharpe Ratio.
rf_returnfloat, default 0: Risk-free rate of return.

Returns:

dict: Weights of assets, risk and return of the tangency portfolio.

Examples

>>> three_assets = ['MCFTR.INDX', 'RGBITR.INDX', 'GC.COMM']
>>> ef = ok.EfficientFrontier(assets=three_assets, ccy='USD', last_date='2022-06')
>>> ef.get_tangency_portfolio(rf_return=0.03)  # risk free rate of return is 3%
{'Weights': array([0.30672901, 0.        , 0.69327099]), 'Mean_return': 0.12265215404959617, 'Risk': 0.1882249366394522}

To calculate tangency portfolio parameters for CAGR (geometric mean) set cagr=True:

>>> ef.get_tangency_portfolio(rate_of_return="mean_return", rf_return=0.03)
{'Weights': array([2.95364739e-01, 1.08420217e-17, 7.04635261e-01]), 'Mean_return': 0.10654206521088283, 'Risk': 0.048279725208422115}

get_most_diversified_portfolio(target_return=None, monthly_return=False)

Calculate assets weights, risk, return and Diversification ratio for the most diversified portfolio given the target return within given bounds.

The most diversified portfolio has the largest Diversification Ratio.

The Diversification Ratio is the ratio of the weighted average of assets risks divided by the portfolio risk. In this case risk is the annuilized standatd deviation for the rate of return .

Parameters:

target_returnfloat, optional: Rate of return value. The optimization process looks for a portfolio with the target_return and largest Diversification ratio. If not sepcifed global most diversified portfolio is obtained. Target return value can be in monthly or annual values depending on ‘monthly_return’ option.
monthly_returnbool, default False: Defines whether to use rate of return monthly (True) or annual (False) values.

Returns:

dict: Weights of assets, risk and return of the most diversified portfolio.

Examples

>>> ls4 = ['SPY.US', 'AGG.US', 'VNQ.US', 'GLD.US']
>>> x = ok.EfficientFrontier(assets=ls4, ccy='USD', last_date='2021-12')
>>> x.get_most_diversified_portfolio()  # get a global most diversified portfolio
{'SPY.US': 0.19612726258395477,
'AGG.US': 0.649730553241489,
'VNQ.US': 0.020096313783052246,
'GLD.US': 0.13404587039150392,
'Mean return': 0.0637820844415733,
'CAGR': 0.062355715886719176,
'Risk': 0.05510135025563423,
'Diversification ratio': 1.5665720501693001}

It is possible to get the most diversified portfolio for a given target rate of return. Set monthly_return=False to use annual values for the rate of return.

>>> x.get_most_diversified_portfolio(target_return=0.10, monthly_return=False)
{'SPY.US': 0.3389762570274293,
'AGG.US': 0.12915657041748244,
'VNQ.US': 0.15083042115027034,
'GLD.US': 0.3810367514048179,
'Mean return': 0.10000000151051025,
'CAGR': 0.09370688842211439,
'Risk': 0.11725067815643951,
'Diversification ratio': 1.4419864802150442}

optimize_return(option='max')

Find a portfolio with global max or min for the rate of return within given bounds.

The objective function is an arithmetic mean of monthly Rate of return.

Bounds are defined with ‘bounds’ property.

Parameters:

option{‘max’, ‘min’}, default ‘max’: Find objective function global maximun if ‘max’ or global minimum if ‘min’.

Returns:

dict: Weights of assets, risk and return of the portfolio.

Examples

>>> ef = ok.EfficientFrontier(['SPY.US', 'AGG.US', 'GLD.US'])
>>> ef.optimize_return(option='max')
{'Weights': array([1.00000000e+00, 1.94289029e-16, 1.11022302e-16]), 'Mean_return_monthly': 0.009144, 'Risk_monthly': 0.041956276163975015}

The global maximum can be found with constrained optimization using bounds.

>>> ef.bounds = ((0, 1.), (0, 1.), (0.20, 1.))  # The portfolio should have at least 20% of GLD
>>> ef.optimize_return(option='max')
{'Weights': array([8.00000000e-01, 5.48172618e-16, 2.00000000e-01]), 'Mean_return_monthly': 0.008894299999999997, 'Risk_monthly': 0.035570987973869726}

minimize_risk(target_return, monthly_return=False, tolerance=1e-08)

Find minimal risk given the target return within given bounds.

In Mean-Variance optimization the objective function is risk (standard deviation of return time series).

Optimization returns a “point” on the Efficient Frontier with values:

weights of assets
annualized mean rate of return
Compound annual growth rate (CAGR)
annualized risk (annualized value of standard deviation)

Target return can have a monthly or annual value.

Bounds are defined with ‘bounds’ property.

Parameters:

target_returnfloat: Rate of return value. The optimization process looks for a portfolio with the target_return and minimum risk. Target return value can be in monthly or annual values depending on ‘monthly_return’ option.
monthly_returnbool, default False: Defines whether to use rate of return monthly (True) or annual (False) values.
tolerancefloat, default 1e-08: Sets the accuracy for the solver.

Returns:

dict: Point on the Efficient Frontier with assets weights, mean return, CAGR, risk.

Examples

>>> ef = ok.EfficientFrontier(['SPY.US', 'AGG.US', 'GLD.US'], last_date='2021-07')
>>> ef.minimize_risk(target_return=0.044, monthly_return=False)
{'SPY.US': 0.03817252986735185,
'AGG.US': 0.9618274701326482,
'GLD.US': 0.0,
'Mean return': 0.04400000000000004,
'CAGR': 0.04335075344214023,
'Risk': 0.037003608635098856}

get_assets_tickers()

property mean_return_range

Calculate the range of mean monthly returns (from min to max).

Number of values in the range is defined by ‘n_points’.

Returns:

numpy.ndarray: Monthly rate of return values from min to max.

Examples

>>> ef = ok.EfficientFrontier(['SPY.US', 'AGG.US', 'GLD.US'], last_date='2021-07')
>>> ef.mean_return_range
array([0.0033745 , 0.00367816, 0.00398182, 0.00428547, 0.00458913,
0.00489279, 0.00519645, 0.00550011, 0.00580376, 0.00610742,
0.00641108, 0.00671474, 0.00701839, 0.00732205, 0.00762571,
0.00792937, 0.00823303, 0.00853668, 0.00884034, 0.009144  ])

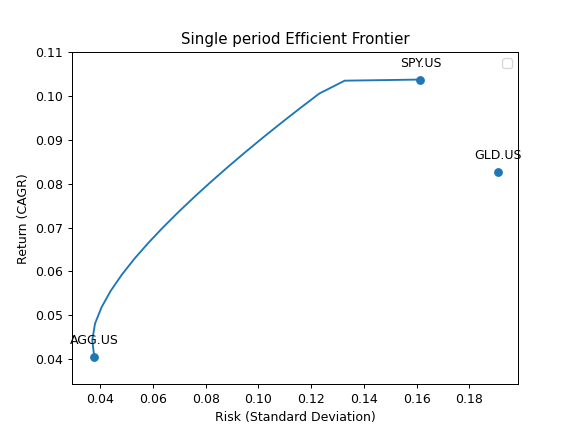
property ef_points

Generate single period Efficient Frontier.

Each point on the Efficient Frontier is a portfolio with optimized risk for a given return.

The points are obtained through the constrained optimization process (optimization with bounds). Bounds are defined with ‘bounds’ property.

Returns:

DataFrame

Table of weights and risk/return values for the Efficient Frontier. The columns:

assets weights
CAGR (geometric mean)
Mean return (arithmetic mean)
Risk (standard deviation)

All the values are annualized.

Examples

>>> assets = ['SPY.US', 'AGG.US', 'GLD.US']
>>> last_date='2021-07'
>>> y = ok.EfficientFrontier(assets, last_date=last_date)
>>> y.ef_points
        Risk  Mean return      CAGR        AGG.US        GLD.US        SPY.US
 0.037707     0.041254  0.040579  1.000000e+00  9.278755e-09  2.220446e-16
 0.036979     0.045042  0.044394  9.473684e-01  0.000000e+00  5.263158e-02
 0.038027     0.048842  0.048157  8.947368e-01  0.000000e+00  1.052632e-01
 0.040517     0.052655  0.051879  8.376442e-01  2.061543e-02  1.417404e-01
 0.043944     0.056481  0.055569  7.801725e-01  4.298194e-02  1.768455e-01
 0.048125     0.060320  0.059229  7.227015e-01  6.534570e-02  2.119528e-01
 0.052902     0.064171  0.062856  6.652318e-01  8.770367e-02  2.470646e-01
 0.058144     0.068035  0.066451  6.077632e-01  1.100558e-01  2.821809e-01
 0.063753     0.071912  0.070014  5.502956e-01  1.324040e-01  3.173004e-01
 0.069655     0.075802  0.073543  4.928283e-01  1.547504e-01  3.524213e-01
0.075796     0.079704  0.077039  4.353613e-01  1.770958e-01  3.875429e-01
0.082136     0.083620  0.080501  3.778987e-01  1.994207e-01  4.226806e-01
0.088645     0.087549  0.083928  3.204253e-01  2.217953e-01  4.577794e-01
0.095300     0.091491  0.087321  2.629559e-01  2.441514e-01  4.928926e-01
0.102084     0.095446  0.090678  2.054869e-01  2.665062e-01  5.280069e-01
0.108984     0.099414  0.093999  1.480175e-01  2.888623e-01  5.631202e-01
0.115991     0.103395  0.097284  9.054789e-02  3.112196e-01  5.982325e-01
0.123096     0.107389  0.100533  3.307805e-02  3.335779e-01  6.333441e-01
0.132674     0.111397  0.103452  0.000000e+00  2.432182e-01  7.567818e-01
0.161413     0.115418  0.103704  1.110223e-16  1.036379e-09  1.000000e+00

To plot the Efficient Frontier use the DataFrame with the points data. Additionaly ‘Plot.plot_assets()’ can be used to show the assets in the chart.

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> # Plot the assets points
>>> y.plot_assets(kind='cagr')  # kind should be set to "cagr" as we take "CAGR" column from the ef_points.
>>> ax = plt.gca()
>>> # Plot the Efficient Frontier
>>> df = y.ef_points
>>> ax.plot(df['Risk'], df['CAGR'])  # we chose to plot CAGR which is geometric mean of return series
>>> # Set the axis labels and the title
>>> ax.set_title('Single period Efficient Frontier')
>>> ax.set_xlabel('Risk (Standard Deviation)')
>>> ax.set_ylabel('Return (CAGR)')
>>> ax.legend()
>>> plt.show()

../_images/okama-EfficientFrontier-1.png

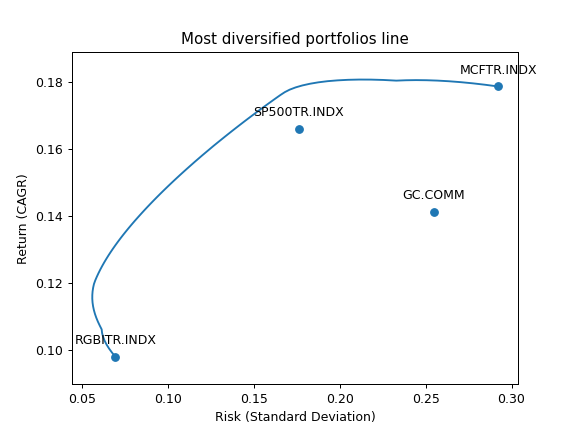
property mdp_points

Generate Most diversified portfolios line.

Each point on the Most diversified portfolios line is a portfolio with optimized Diversification ratio for a given return.

The points are obtained through the constrained optimization process (optimization with bounds). Bounds are defined with ‘bounds’ property.

Returns:

DataFrame

Table of weights and risk/return values for the Efficient Frontier. The columns:

assets weights
CAGR (geometric mean)
Mean return (arithmetic mean)
Risk (standard deviation)
Diversification ratio

All the values are annualized.

Examples

>>> ls4 = ['SP500TR.INDX', 'MCFTR.INDX', 'RGBITR.INDX', 'GC.COMM']
>>> y = ok.EfficientFrontier(assets=ls4, ccy='RUB', last_date='2021-12', n_points=100)
>>> y.mdp_points  # print mdp weights, risk, mean return, CAGR and Diversification ratio
        Risk  Mean return      CAGR  ...    MCFTR.INDX   RGBITR.INDX  SP500TR.INDX
0   0.066040     0.094216  0.092220  ...  2.081668e-16  1.000000e+00  0.000000e+00
1   0.064299     0.095342  0.093451  ...  0.000000e+00  9.844942e-01  5.828671e-16
2   0.062761     0.096468  0.094670  ...  0.000000e+00  9.689885e-01  1.110223e-16
3   0.061445     0.097595  0.095874  ...  5.828671e-16  9.534827e-01  0.000000e+00
4   0.060364     0.098724  0.097065  ...  3.191891e-16  9.379769e-01  0.000000e+00
..       ...          ...       ...  ...           ...           ...           ...
95  0.258857     0.205984  0.178346  ...  8.840844e-01  1.387779e-17  0.000000e+00
96  0.266583     0.207214  0.177941  ...  9.130633e-01  3.469447e-18  0.000000e+00
97  0.274594     0.208446  0.177432  ...  9.420422e-01  0.000000e+00  1.075529e-16
98  0.282873     0.209678  0.176820  ...  9.710211e-01  2.428613e-17  6.938894e-18
99  0.291402     0.210912  0.176103  ...  1.000000e+00  2.775558e-16  3.951094e-09
[100 rows x 8 columns]

To plot the Most diversification portfolios line use the DataFrame with the points data. Additionaly ‘Plot.plot_assets()’ can be used to show the assets in the chart.

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> # Plot the assets points
>>> y.plot_assets(kind='cagr')  # kind should be set to "cagr" as we take "CAGR" column from the ef_points.
>>> ax = plt.gca()
>>> # Plot the Most diversified portfolios line
>>> df = y.mdp_points
>>> ax.plot(df['Risk'], df['CAGR'])  # we chose to plot CAGR which is geometric mean of return series
>>> # Set the axis labels and the title
>>> ax.set_title('Most diversified portfolios line')
>>> ax.set_xlabel('Risk (Standard Deviation)')
>>> ax.set_ylabel('Return (CAGR)')
>>> plt.show()

../_images/okama-EfficientFrontier-2.png

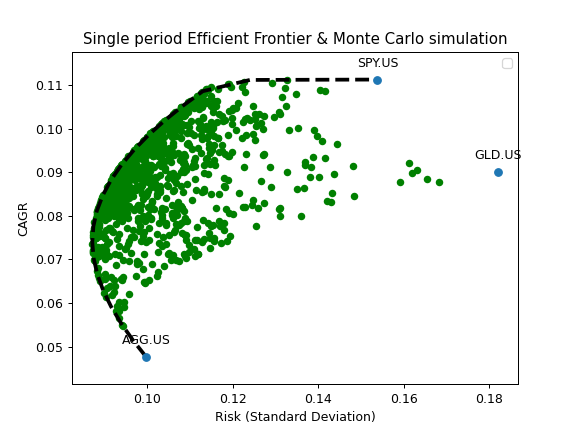
get_monte_carlo(n=100, kind='mean')

Generate N random portfolios with Monte Carlo simulation.

Risk (annualized standard deviation) and Return (CAGR) are calculated for a set of random weights.

Parameters:

nint, default 100: Number of random portfolios to generate with Monte Carlo simulation.
kind{‘mean’,’cagr’}, default ‘mean’: Use CAGR for return if kind=’cagr’, or annualized arithmetic mean if kind=’mean’.

Returns:

DataFrame: Table with Return, Risk and weights values for random portfolios.

Examples

>>> assets = ['SPY.US', 'AGG.US', 'GLD.US']
>>> last_date='2021-07'
>>> base_currency = 'EUR'
>>> y = ok.EfficientFrontier(assets, ccy=base_currency, last_date=last_date)
>>> y.get_monte_carlo(n=10)  # generate 10 random portfolios
       Risk    Return    SPY.US    AGG.US    GLD.US
0  0.099168  0.101667  0.470953  0.205227  0.323819
1  0.099790  0.076282  0.070792  0.558928  0.370280
2  0.129312  0.106620  0.274261  0.050524  0.675215
3  0.102031  0.083311  0.129375  0.443444  0.427182
4  0.102956  0.105136  0.489213  0.146174  0.364614
5  0.095690  0.091834  0.297122  0.335066  0.367812
6  0.103747  0.090285  0.203408  0.334694  0.461898
7  0.148311  0.099617  0.082660  0.120871  0.796470
8  0.115780  0.082983  0.042871  0.422335  0.534794
9  0.093903  0.088553  0.266303  0.387332  0.346365

To plot Monte Carlo simulation result it’s useful to combine in with the Efficien Frontier chart. Additionaly assets points could be plotted with ‘Plot.plot_assets()’.

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> # Plot the assets points (optional).
>>> # The same first and last dates, base currency and return type should be used.
>>> y.plot_assets(kind='cagr')
>>> ax = plt.gca()
>>> # Plot random portfolios risk-return points.
>>> mc = y.get_monte_carlo(n=1000, kind='cagr')
>>> ax.scatter(mc.Risk, mc.CAGR, linewidth=0, color='green')
>>> # Plot the Efficient (optional)
>>> df = y.ef_points
>>> ax.plot(df['Risk'], df['CAGR'], color='black', linestyle='dashed', linewidth=3)
>>> # Set the title and axis labels
>>> ax.set_title('Single period Efficient Frontier & Monte Carlo simulation')
>>> ax.set_xlabel('Risk (Standard Deviation)')
>>> ax.set_ylabel('CAGR')
>>> ax.legend()
>>> plt.show()

../_images/okama-EfficientFrontier-3.png

plot_transition_map(x_axe='risk', figsize=None)

Plot Transition Map for optimized portfolios on the single period Efficient Frontier.

Transition Map shows the relation between asset weights and optimized portfolios properties:

CAGR (Compound annual growth rate)
Risk (annualized standard deviation of return)

Wights are displayed on the y-axis. CAGR or Risk - on the x-axis.

Constrained optimization with weights bounds is available.

Parameters:

boundstuple of ((float, float),…): Bounds for the assets weights. Each asset can have weights limitation from 0 to 1.0. If an asset has limitation for 10 to 20%, bounds are defined as (0.1, 0.2). bounds = ((0, .5), (0, 1)) shows that in Portfolio with two assets first one has weight limitations from 0 to 50%. The second asset has no limitations.
x_axe{‘risk’, ‘cagr’}, default ‘risk’: Show the relation between weights and CAGR (if ‘cagr’) or between weights and Risk (if ‘risk’). CAGR or Risk are displayed on the x-axis.
figsize(float, float), optional: Figure size: width, height in inches. If None default matplotlib size is taken: [6.4, 4.8]

Returns:

Axes‘matplotlib.axes._subplots.AxesSubplot’

Examples

>>> import matplotlib.pyplot as plt
>>> x = ok.EfficientFrontier(['SPY.US', 'AGG.US', 'GLD.US'], ccy='USD', inflation=False)
>>> x.plot_transition_map()
>>> plt.show()

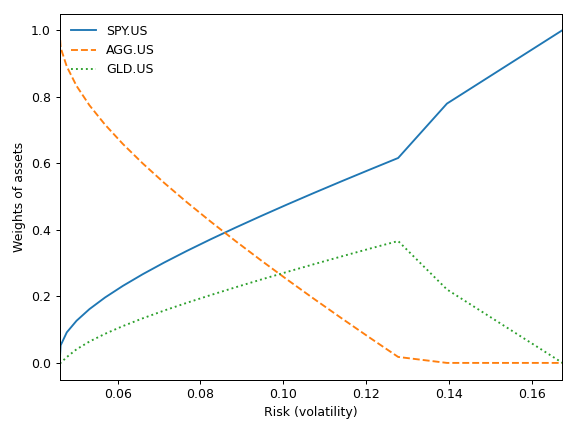
../_images/okama-EfficientFrontier-4_00_00.png

Transition Map with default setting show the relation between Risk (stanrd deviation) and assets weights for optimized portfolios. The same relation for CAGR can be shown setting x_axe=’cagr’.

>>> x.plot_transition_map(x_axe='cagr')
>>> plt.show()

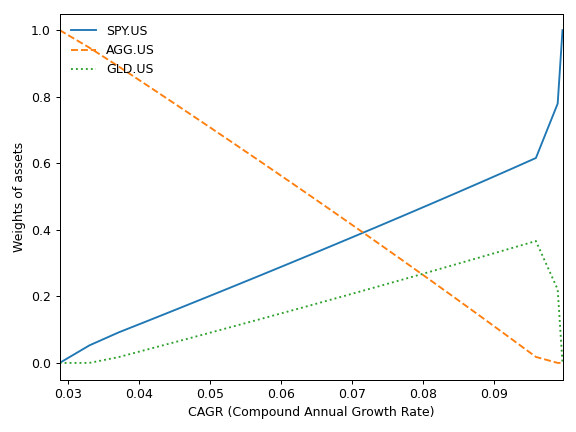
../_images/okama-EfficientFrontier-4_01_00.png

property annual_return_ts

Calculate annual rate of return time series for each asset.

Rate of return is calculated for each calendar year.

Returns:

DataFrame: Calendar annual rate of return time series.

Examples

>>> import matplotlib.pyplot as plt
>>> al = ok.AssetList(['SPY.US', 'BND.US'], last_date='2021-08')
>>> al.annual_return_ts.plot(kind='bar')
>>> plt.show()

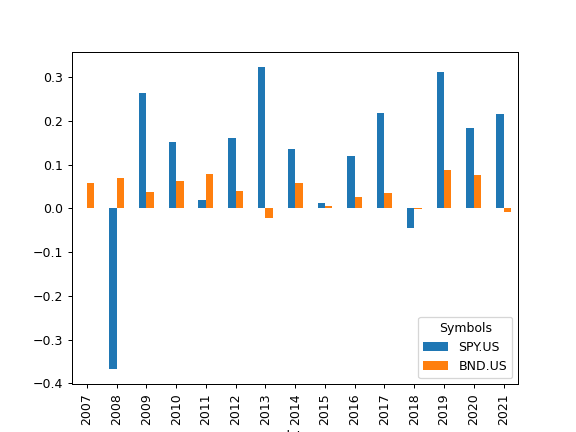
../_images/okama-EfficientFrontier-5.png

property currency

Return the base currency of the Asset List.

Such properties as rate of return and risk are adjusted to the base currency.

Returns:

okama.Asset: Base currency of the Asset List in form of okama.Asset class.

describe(years=(1, 5, 10), tickers=True)

Generate descriptive statistics for a list of assets.

Statistics includes:

YTD (Year To date) compound return
CAGR for a given list of periods and full available period
Annualized mean rate of return (full available period)
LTM Dividend yield - last twelve months dividend yield

Risk metrics (full period):

risk (standard deviation)
CVAR (timeframe is 1 year)
max drawdowns (and dates of the drawdowns)

Statistics also shows for each asset: - inception date - first date available for each asset - last asset date - available for each asset date - Common last data date - common for the asset list data (may be set by last_date manually)

Parameters:

yearstuple of (int,), default (1, 5, 10): List of periods for CAGR.
tickersbool, default True: Defines whether show tickers (True) or assets names in the header.

Returns:

DataFrame: Table of descriptive statistics for a list of assets.

See also

get_cumulative_return: Calculate cumulative return.
get_cagr: Calculate assets Compound Annual Growth Rate (CAGR).
dividend_yield: Calculate dividend yield (LTM).
risk_annual: Return annualized risks (standard deviation).
get_cvar: Calculate historic Conditional Value at Risk (CVAR, expected shortfall).
drawdowns: Calculate drawdowns.

Examples

>>> al = ok.AssetList(['SPY.US', 'AGG.US'], last_date='2021-08')
>>> al.describe(years=[1, 10, 15])
                 property               period    AGG.US    SPY.US inflation
       Compound return                  YTD -0.005620  0.180519  0.048154
                  CAGR              1 years -0.007530  0.363021  0.053717
                  CAGR             10 years  0.032918  0.152310  0.019136
                  CAGR             15 years  0.043013  0.107598  0.019788
                  CAGR  17 years, 10 months  0.039793  0.107972  0.022002
        Dividend yield                  LTM  0.018690  0.012709       NaN
                  Risk  17 years, 10 months  0.037796  0.158301       NaN
                  CVAR  17 years, 10 months  0.023107  0.399398       NaN

property dividend_growing_years

Return the number of years when the annual dividend was growing for each asset.

Returns:

DataFrame: Dividend growth length periods time series for each asset.

See also

dividend_yield: Dividend yield time series.
dividend_yield_annual: Calendar year dividend yield time series.
dividends_annual: Calendar year dividends.
dividend_paying_years: Number of years of consecutive dividend payments.
get_dividend_mean_yield: Arithmetic mean for annual dividend yield.
get_dividend_mean_growth_rate: Geometric mean of annual dividends growth rate.

Examples

>>> import matplotlib.pyplot as plt
>>> x = ok.AssetList(['T.US', 'XOM.US'], first_date='1984-01', last_date='1994-12')
>>> x.dividend_growing_years.plot(kind='bar')
>>> plt.show()

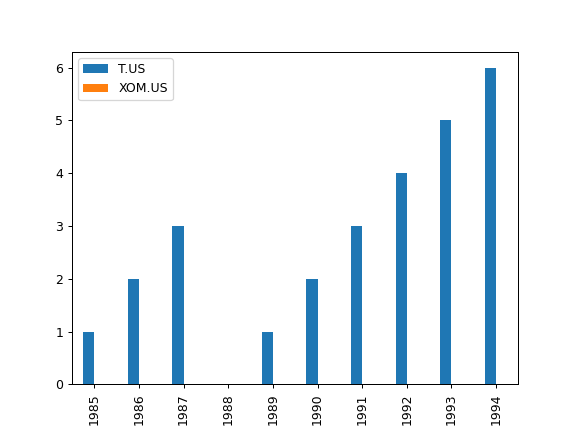
../_images/okama-EfficientFrontier-6.png

property dividend_paying_years

Return the number of years of consecutive dividend payments for each asset.

Returns:

DataFrame: Dividend payment period length time series for each asset.

See also

dividend_yield: Dividend yield time series.
dividend_yield_annual: Calendar year dividend yield time series.
dividends_annual: Calendar year dividends.
dividend_growing_years: Number of years when the annual dividend was growing.
get_dividend_mean_yield: Arithmetic mean for annual dividend yield.
get_dividend_mean_growth_rate: Geometric mean of annual dividends growth rate.

Examples

>>> import matplotlib.pyplot as plt
>>> x = ok.AssetList(['T.US', 'XOM.US'], first_date='1984-01', last_date='1994-12')
>>> x.dividend_paying_years.plot(kind='bar')
>>> plt.show()

../_images/okama-EfficientFrontier-7.png

property dividend_yield

Calculate last twelve months (LTM) dividend yield time series (monthly) for each asset.

LTM dividend yield is the sum trailing twelve months of common dividends per share divided by the current price per share.

All yields are calculated in the asset list base currency after adjusting the dividends and price time series. Forecasted (future) dividends are removed. Zero value time series are created for assets without dividends.

Returns:

DataFrame: Time series of LTM dividend yield for each asset.

See also

dividend_yield_annual: Calendar year dividend yield time series.
dividends_annual: Calendar year dividends time series.
dividend_paying_years: Number of years of consecutive dividend payments.
dividend_growing_years: Number of years when the annual dividend was growing.
get_dividend_mean_yield: Arithmetic mean for annual dividend yield.
get_dividend_mean_growth_rate: Geometric mean of annual dividends growth rate.

Examples

>>> x = ok.AssetList(['T.US', 'XOM.US'], first_date='1984-01', last_date='1994-12')
>>> x.dividend_yield
           T.US    XOM.US
1984-01  0.000000  0.000000
1984-02  0.000000  0.002597
1984-03  0.002038  0.002589
1984-04  0.001961  0.002346
           ...       ...
1994-09  0.018165  0.012522
1994-10  0.018651  0.011451
1994-11  0.018876  0.012050
1994-12  0.019344  0.011975
[132 rows x 2 columns]

property dividend_yield_annual

Calculate last twelve months (LTM) dividend yield annual time series.

Time series is based on the dividend yield for the end of calendar year.

LTM dividend yield is the sum trailing twelve months of common dividends per share divided by the current price per share.

All yields are calculated in the asset list base currency after adjusting the dividends and price time series. Forecasted (future) dividends are removed.

Returns:

DataFrame: Time series of LTM dividend yield for each asset.

See also

dividend_yield: Dividend yield time series.
dividends_annual: Calendar year dividends time series.
dividend_paying_years: Number of years of consecutive dividend payments.
dividend_growing_years: Number of years when the annual dividend was growing.
get_dividend_mean_yield: Arithmetic mean for annual dividend yield.
get_dividend_mean_growth_rate: Geometric mean of annual dividends growth rate.

Examples

>>> import matplotlib.pyplot as plt
>>> x = ok.AssetList(['T.US', 'XOM.US'], first_date='2010-01', last_date='2020-12')
>>> x.dividend_yield_annual.plot(kind='bar')
>>> plt.show()

../_images/okama-EfficientFrontier-8.png

property dividends_annual

Return calendar year dividends sum time series for each asset.

Returns:

DataFrame: Annual dividends time series for each asset.

See also

dividend_yield: Dividend yield time series.
dividend_yield_annual: Calendar year dividend yield time series.
dividend_paying_years: Number of years of consecutive dividend payments.
dividend_growing_years: Number of years when the annual dividend was growing.
get_dividend_mean_yield: Arithmetic mean for annual dividend yield.
get_dividend_mean_growth_rate: Geometric mean of annual dividends growth rate.

Examples

>>> import matplotlib.pyplot as plt
>>> x = ok.AssetList(['T.US', 'XOM.US'], first_date='2010-01', last_date='2020-12')
>>> x.dividends_annual.plot(kind='bar')
>>> plt.show()

../_images/okama-EfficientFrontier-9.png

property drawdowns

Calculate drawdowns time series for the assets.

The drawdown is the percent decline from a previous peak in wealth index.

Returns:

DataFrame: Time series of drawdowns.

See also

risk_monthly: Calculate montly risk for each asset.
risk_annual: Calculate annualized risks.
semideviation_monthly: Calculate semideviation monthly values.
semideviation_annual: Calculate semideviation annualized values.
get_var_historic: Calculate historic Value at Risk (VaR).
get_cvar_historic: Calculate historic Conditional Value at Risk (CVaR).

Examples

>>> import matplotlib.pyplot as plt
>>> al = ok.AssetList(['SPY.US', 'BND.US'], last_date='2021-08')
>>> al.drawdowns.plot()
>>> plt.show()

../_images/okama-EfficientFrontier-10.png

get_cagr(period=None, real=False)

Calculate assets Compound Annual Growth Rate (CAGR) for a given trailing period.

Compound annual growth rate (CAGR) is the rate of return that would be required for an investment to grow from its initial to its final value, assuming all incomes were reinvested.

Inflation adjusted annualized returns (real CAGR) are shown with real=True option.

Annual inflation value is calculated for the same period if inflation=True in the AssetList.

Parameters:

period: int, optional: CAGR trailing period in years. None for the full time CAGR.
real: bool, default False: CAGR is adjusted for inflation (real CAGR) if True. AssetList should be initiated with Inflation=True for real CAGR.

Returns:

Series: CAGR values for each asset and annualized inflation (optional).

See also

get_rolling_cagr: Calculate rolling CAGR.

Notes

CAGR is not defined for periods less than 1 year (NaN values are returned).

Examples

>>> x = ok.AssetList()
>>> x.get_cagr(period=5)
SPY.US    0.1510
USD.INFL   0.0195
dtype: float64

To get inflation adjusted return (real annualized return) add real=True option:

>>> x = ok.AssetList(['EURUSD.FX', 'CNYUSD.FX'], inflation=True)
>>> x.get_cagr(period=5, real=True)
EURUSD.FX    0.000439
CNYUSD.FX   -0.017922
dtype: float64

get_cumulative_return(period=None, real=False)

Calculate cumulative return over a given trailing period for each asset.

The cumulative return is the total change in the asset price during the investment period.

Inflation adjusted cumulative returns (real cumulative returns) are shown with real=True option. Annual inflation data is calculated for the same period if inflation=True in the AssetList.

Parameters:

period: str, int or None, default None: Trailing period in years. Period should be more then 0. None - full time cumulative return. ‘YTD’ - (Year To Date) period of time beginning the first day of the calendar year up to the last month.
real: bool, default False: Cumulative return is adjusted for inflation (real cumulative return) if True. AssetList should be initiated with Inflation=True for real cumulative return.

Returns:

Series: Cumulative return values for each asset and cumulative inflation (if inflation=True in AssetList).

See also

get_rolling_cagr: Calculate rolling CAGR.
get_cagr: Calculate CAGR.
get_rolling_cumulative_return: Calculate rolling cumulative return.
annual_return: Calculate annualized mean return (arithmetic mean).

Examples

>>> x = ok.AssetList(['MCFTR.INDX'], ccy='RUB')
>>> x.get_cumulative_return(period='YTD')
MCFTR.INDX   0.1483
RUB.INFL     0.0485
dtype: float64

get_cvar_historic(time_frame=12, level=1)

Calculate historic Conditional Value at Risk (CVAR, expected shortfall) for the assets with a given timeframe.

CVaR is the average loss over a specified time period of unlikely scenarios beyond the confidence level. Loss is a positive number (expressed in cumulative return). If CVaR is negative there are expected gains at this confidence level.

Parameters:

time_frameint, default 12: Time period size in months
levelint, default 1: Confidence level in percents to calculate the VaR. Default value is 1% (1% quantile).

Returns:

Series: CVaR values for each asset in form of Series.

See also

risk_monthly: Calculate montly risk for each asset.
risk_annual: Calculate annualized risks.
semideviation_monthly: Calculate semideviation monthly values.
semideviation_annual: Calculate semideviation annualized values.
get_var_historic: Calculate historic Value at Risk (VaR).
drawdowns: Calculate drawdowns.

Examples

>>> x = ok.AssetList(['SPY.US', 'AGG.US'])
>>> x.get_cvar_historic(time_frame=60, level=1)
SPY.US    0.2574
AGG.US   -0.0766
dtype: float64
Name: VaR, dtype: float64

get_dividend_mean_growth_rate(period=5)

Calculate geometric mean of annual dividends growth rate time series for a given trailing period.

Growth rate is taken for full calendar annual dividends.

Parameters:

periodint, default 5: Growth rate trailing period in years. Period should be a positive integer and not exceed the available data period_length.

Returns:

Series: Dividend growth geometric mean value for each asset.

See also

dividend_yield: Dividend yield time series.
dividend_yield_annual: Calendar year dividend yield time series.
dividends_annual: Calendar year dividends.
dividend_paying_years: Number of years of consecutive dividend payments.
dividend_growing_years: Number of years when the annual dividend was growing.
get_dividend_mean_yield: Arithmetic mean for annual dividend yield.

Examples

>>> x = ok.AssetList(['T.US', 'XOM.US'], first_date='1984-01', last_date='1994-12')
>>> x.get_dividend_mean_growth_rate(period=3)
T.US      0.020067
XOM.US    0.024281
dtype: float64

get_dividend_mean_yield(period=5)

Calculate the arithmetic mean for annual dividend yield (LTM) over a specified period.

Dividend yield is taken for full calendar annual dividends.

Parameters:

periodint, default 5: Mean dividend yield trailing period in years. Period should be a positive integer and not exceed the available data period_length.

Returns:

Series: Mean dividend yield value for each asset.

See also

dividend_yield: Dividend yield time series.
dividend_yield_annual: Calendar year dividend yield time series.
dividends_annual: Calendar year dividends.
get_dividend_mean_growth_rate: Geometric mean of annual dividends growth rate.
dividend_paying_years: Number of years of consecutive dividend payments.
dividend_growing_years: Number of years when the annual dividend was growing.

Examples

>>> al = ok.AssetList(["SBERP.MOEX", "LKOH.MOEX"], ccy='RUB', first_date='2005-01', last_date='2023-12')
>>> al.get_dividend_mean_yield(period=3)
SBERP.MOEX    0.052987
LKOH.MOEX     0.156526
dtype: float64

get_rolling_cagr(window=12, real=False)

Calculate rolling CAGR for each asset.

Compound annual growth rate (CAGR) is the rate of return that would be required for an investment to grow from its initial to its final value, assuming all incomes were reinvested.

Inflation adjusted annualized returns (real CAGR) are shown with real=True option.

Parameters:

windowint, default 12: Size of the moving window in months. Window size should be at least 12 months for CAGR.
real: bool, default False: CAGR is adjusted for inflation (real CAGR) if True. AssetList should be initiated with Inflation=True for real CAGR.

Returns:

DataFrame: Time series of rolling CAGR and mean inflation (optionally).

See also

get_rolling_cagr: Calculate rolling CAGR.
get_cagr: Calculate CAGR.
get_rolling_cumulative_return: Calculate rolling cumulative return.
annual_return: Calculate annualized mean return (arithmetic mean).

Notes

CAGR is not defined for periods less than 1 year (NaN values are returned).

Examples

>>> import matplotlib.pyplot as plt
>>> x = ok.AssetList(['SPY.US', 'AGG.US'], ccy='USD', inflation=True)
>>> x.get_rolling_cagr(window=5*12).plot()
>>> plt.show()

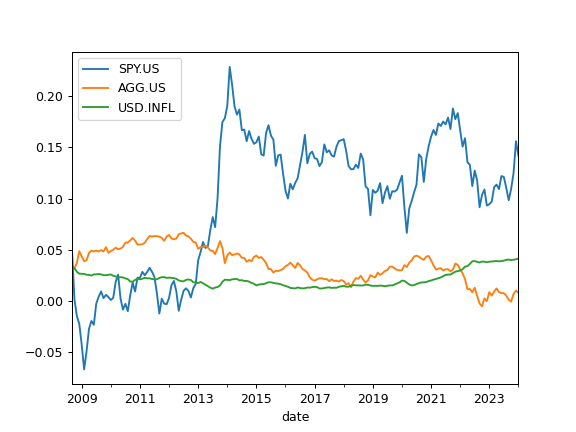
../_images/okama-EfficientFrontier-11_00_00.png

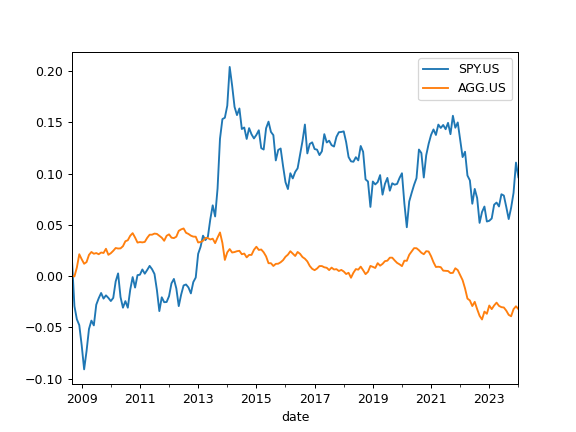
For inflation adjusted rolling CAGR add ‘real=True’ option:

>>> x.get_rolling_cagr(window=5*12, real=True).plot()
>>> plt.show()

../_images/okama-EfficientFrontier-11_01_00.png

get_rolling_cumulative_return(window=12, real=False)

Calculate rolling cumulative return for each asset.

The cumulative return is the total change in the asset price.

Parameters:

windowint, default 12: Size of the moving window in months.
real: bool, default False: Cumulative return is adjusted for inflation (real cumulative return) if True. AssetList should be initiated with Inflation=True for real cumulative return.

Returns:

DataFrame: Time series of rolling cumulative return.

See also

get_rolling_cagr: Calculate rolling CAGR.
get_cagr: Calculate CAGR.
get_cumulative_return: Calculate cumulative return.
annual_return: Calculate annualized mean return (arithmetic mean).

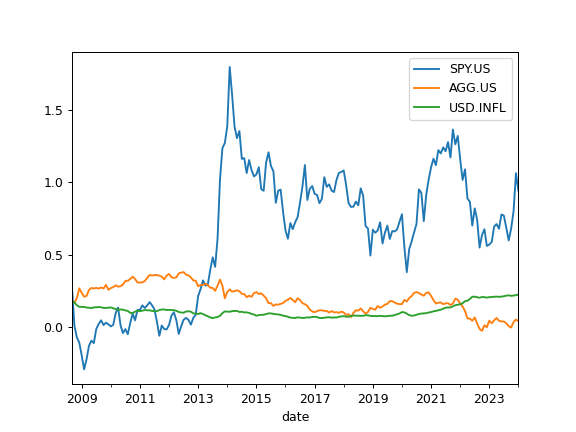
Examples

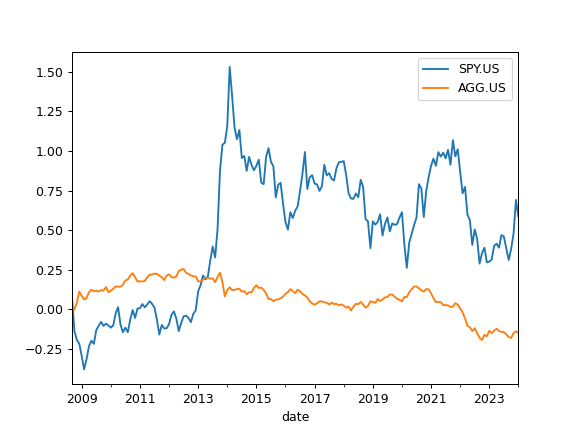
>>> import matplotlib.pyplot as plt
>>> x = ok.AssetList(['SPY.US', 'AGG.US'], ccy='USD', inflation=True)
>>> x.get_rolling_cumulative_return(window=5*12).plot()
>>> plt.show()

../_images/okama-EfficientFrontier-12_00_00.png

For inflation adjusted rolling cumulative return add ‘real=True’ option:

>>> x.get_rolling_cumulative_return(window=5*12, real=True).plot()
>>> plt.show()

../_images/okama-EfficientFrontier-12_01_00.png

get_rolling_risk_annual(window=12)

Calculate annualized risk rolling time series for each asset.

Risk is a standard deviation of the rate of return.

Annualized risk time series is calculated for the rate of return values limited by moving window.

Parameters:

windowint, default 12: Size of the moving window in months.

Returns:

DataFrame: Annualized risk (standard deviation) rolling time series for each asset.

See also

risk_monthly: Calculate montly risk expanding time series for each asset.
risk_annual: Calculate annualized risks.
semideviation_monthly: Calculate semideviation monthly values.
semideviation_annual: Calculate semideviation annualized values.
get_var_historic: Calculate historic Value at Risk (VaR).
get_cvar_historic: Calculate historic Conditional Value at Risk (CVaR).
drawdowns: Calculate assets drawdowns.

Examples

>>> import matplotlib.pyplot as plt
>>> x = ok.AssetList(['SPY.US', 'AGG.US'], ccy='USD', inflation=True)
>>> x.get_rolling_risk_annual(window=5*12).plot()
>>> plt.show()

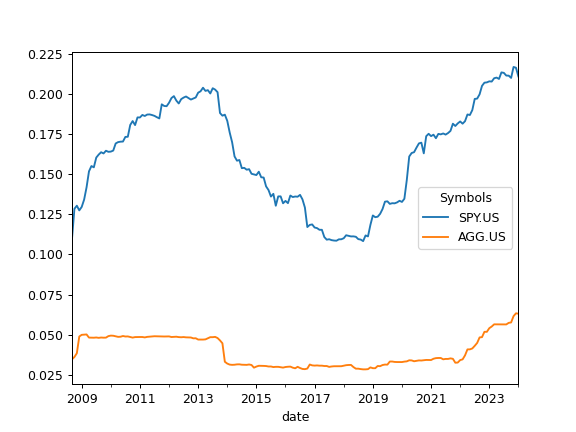
../_images/okama-EfficientFrontier-13.png

get_sharpe_ratio(rf_return=0)

Calculate Sharpe ratio for the assets.

The Sharpe ratio is the average annual return in excess of the risk-free rate per unit of risk (annualized standard deviation).

Risk-free rate should be taken according to the AssetList base currency.

Parameters:

rf_returnfloat, default 0: Risk-free rate of return.

Returns:

pd.Series

Examples

>>> al = ok.AssetList(['VOO.US', 'BND.US'])
>>> al.get_sharpe_ratio(rf_return=0.02)
VOO.US    0.962619
BND.US    0.390814
dtype: float64

get_sortino_ratio(t_return=0)

Calculate Sortino ratio for the assets with specified target return.

Sortion ratio measures the risk-adjusted return of each asset. It is a modification of the Sharpe ratio but penalizes only those returns falling below a specified target rate of return, while the Sharpe ratio penalizes both upside and downside volatility equally.

Parameters:

t_returnfloat, default 0: Traget rate of return.

Returns:

pd.Series

Examples

>>> al = ok.AssetList(['VOO.US', 'BND.US'], last_date='2021-12')
>>> al.get_sortino_ratio(t_return=0.03)
VOO.US    1.321951
BND.US    0.028969
dtype: float64

get_var_historic(time_frame=12, level=1)

Calculate historic Value at Risk (VaR) for the assets with a given timeframe.

The VaR calculates the potential loss of an investment with a given time frame and confidence level. Loss is a positive number (expressed in cumulative return). If VaR is negative there are expected gains at this confidence level.

Parameters:

time_frameint, default 12: Time period size in months
levelint, default 1: Confidence level in percents. Default value is 1%.

Returns:

Series: VaR values for each asset in form of Series.

See also

risk_monthly: Calculate montly risk for each asset.
risk_annual: Calculate annualized risks.
semideviation_monthly: Calculate semideviation monthly values.
semideviation_annual: Calculate semideviation annualized values.
get_cvar_historic: Calculate historic Conditional Value at Risk (CVaR).
drawdowns: Calculate drawdowns.

Examples

>>> x = ok.AssetList(['SPY.US', 'AGG.US'])
>>> x.get_var_historic(time_frame=60, level=1)
SPY.US    0.2101
AGG.US    -0.0867
Name: VaR, dtype: float64

index_beta(rolling_window=None)

Compute beta coefficient time series for the assets.

Beta coefficient is defined in Capital Asset Pricing Model (CAPM). It is a measure of how an individual asset moves (on average) when the benchmark increases or decreases. When beta is positive, the asset price tends to move in the same direction as the benchmark, and the magnitude of beta tells by how much.

Index (benchmark) should be in the first position of the symbols list in AssetList parameters. There should be at least 12 months of historical data.

Parameters:

rolling_windowint or None, default None: Size of the moving window in months. Must be at least 12 months. If None calculate expanding beta coefficient.

Returns:

DataFrame: rollinf or expanding beta coefficient time series for each asset.

See also

index_corr: Compute correlation with the index (or benchmark).
index_rolling_corr: Compute rolling correlation with the index (or benchmark).
index_beta: Compute beta coefficient.

Examples

>>> import matplotlib.pyplot as plt
>>> sp = ok.AssetList(['SP500TR.INDX', 'VBMFX.US', 'GC.COMM', 'VNQ.US'])
>>> sp.names
{'SP500TR.INDX': 'S&P 500 (TR)',
'VBMFX.US': 'VANGUARD TOTAL BOND MARKET INDEX FUND INVESTOR SHARES',
'GC.COMM': 'Gold',
'VNQ.US': 'Vanguard Real Estate Index Fund ETF Shares'}
>>> sp.index_beta().plot()
>>> plt.show()

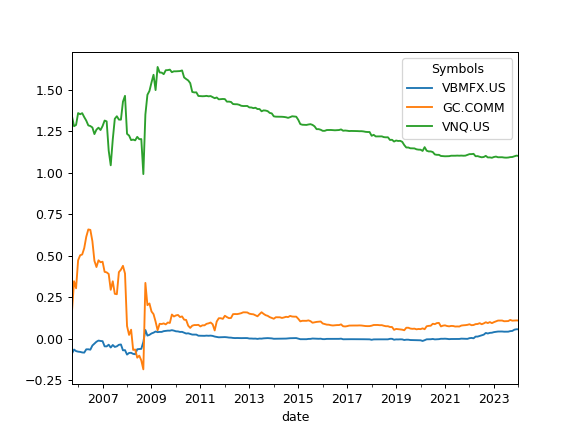
../_images/okama-EfficientFrontier-14_00_00.png

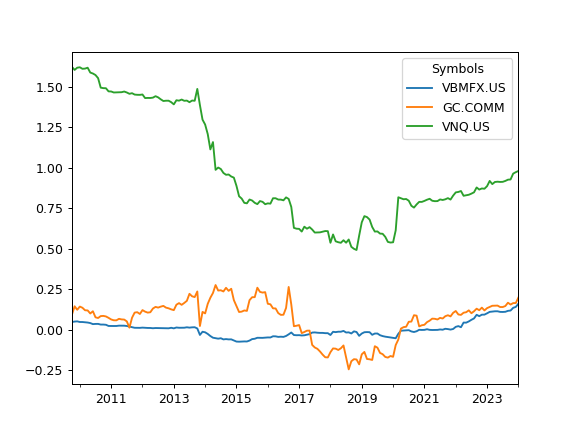
To calculate rolling beta set rolling_window to a number of months (moving window size):

>>> sp.index_beta(rolling_window = 12 * 5).plot()  # 5 years moving window
>>> plt.show()

../_images/okama-EfficientFrontier-14_01_00.png

index_corr(rolling_window=None)

Compute correlation with the index (or benchmark) time series for the assets. Expanding or rolling correlation is available.

Index (benchmark) should be in the first position of the symbols list in AssetList parameters. There should be at least 12 months of historical data.

Parameters:

rolling_windowint or None, default None: Size of the moving window in months. Must be at least 12 months. If None calculate expanding correlation with index.

Returns:

DataFrame: Rolling or expanding correlation with the index (or benchmark) time series for each asset.

Examples

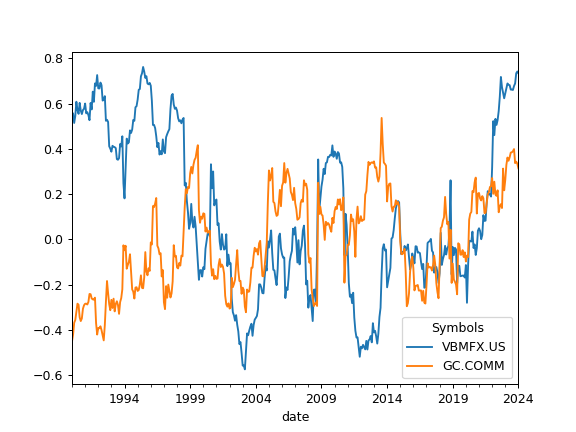
>>> import matplotlib.pyplot as plt
>>> sp = ok.AssetList(['SP500TR.INDX', 'VBMFX.US', 'GC.COMM'])
>>> sp.names
{'SP500TR.INDX': 'S&P 500 (TR)',
'VBMFX.US': 'VANGUARD TOTAL BOND MARKET INDEX FUND INVESTOR SHARES',
'GC.COMM': 'Gold'}
>>> sp.index_corr().plot()  # expanding correlation with S&P 500
>>> plt.show()

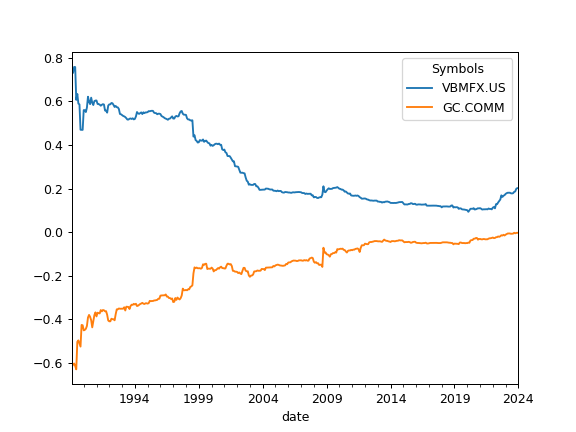
../_images/okama-EfficientFrontier-15_00_00.png

To calculate rolling correlation with S&P 500 set rolling_window to a number of months (moving window size):

>>> sp.index_corr(rolling_window=24).plot()
>>> plt.show()

../_images/okama-EfficientFrontier-15_01_00.png

property jarque_bera

Perform Jarque-Bera test for normality of assets returns historical data.

Jarque-Bera test shows whether the returns have the skewness and kurtosis matching a normal distribution (null hypothesis or H0).

Returns:

DataFrame: Returns test statistic and the p-value for the hypothesis test. large Jarque-Bera statistics and tiny p-value indicate that null hypothesis (H0) is rejected and the time series are not normally distributed. Low statistic numbers correspond to normal distribution.

See also

skewness: Compute skewness.
skewness_rolling: Compute rolling skewness.
kurtosis: Calculate expanding Fisher (normalized) kurtosis.
kurtosis_rolling: Calculate rolling Fisher (normalized) kurtosis.
kstest: Perform Kolmogorov-Smirnov test for different types of distributions.

Examples

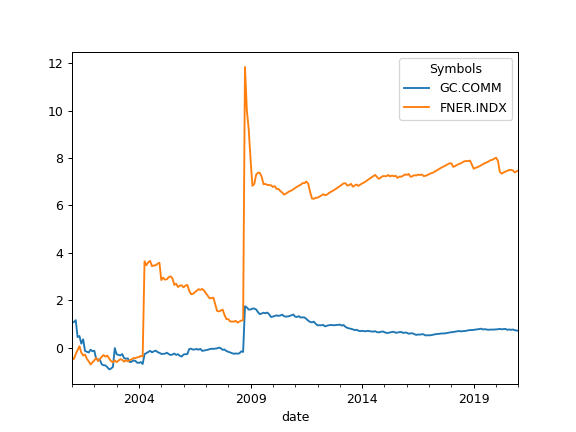
>>> al = ok.AssetList(['GC.COMM', 'FNER.INDX'], first_date='2000-01', last_date='2021-01')
>>> al.names
{'GC.COMM': 'Gold',
'FNER.INDX': 'FTSE NAREIT All Equity REITs'}
>>> al.jarque_bera
            GC.COMM   FNER.INDX
statistic  4.507287  593.633047
p-value    0.105016    0.000000

Gold return time series (GC.COMM) distribution have small p-values (H0 is not rejected). Null hypothesis (H0) is rejected for FTSE NAREIT Index (FNER.INDX) as Jarque-Bera test shows very small p-value and large statistic.

kstest(distr='norm')

Perform Kolmogorov-Smirnov test for goodness of fit the asset returns to a given distribution.

Kolmogorov-Smirnov is a test of the distribution of assets returns historical data against a given distribution. Under the null hypothesis (H0), the two distributions are identical.

Parameters:

distr{‘norm’, ‘lognorm’}, default ‘norm’: Type of distributions. Can be ‘norm’ - for normal distribution or ‘lognorm’ - for lognormal distribtion.

Returns:

DataFrame: Returns test statistic and the p-value for the hypothesis test. Large test statistics and tiny p-value indicate that null hypothesis (H0) is rejected.

Examples

>>> al = ok.AssetList(['EDV.US'], last_date='2021-01')
>>> al.kstest(distr='lognorm')
             EDV.US
p-value    0.402179
statistic  0.070246

H0 is not rejected for EDV ETF and it seems to have lognormal distribution.

property kurtosis

Calculate expanding Fisher (normalized) kurtosis of the return time series for each asset.

Kurtosis is the fourth central moment divided by the square of the variance. It is a measure of the “tailedness” of the probability distribution of a real-valued random variable.

Kurtosis should be close to zero for normal distribution.

Returns:

DataFrame: Expanding kurtosis time series for each asset.

See also

skewness: Compute skewness.
skewness_rolling: Compute rolling skewness.
kurtosis_rolling: Calculate rolling Fisher (normalized) kurtosis.
jarque_bera: Perform Jarque-Bera test for normality.
kstest: Perform Kolmogorov-Smirnov test for different types of distributions.

Examples

>>> import matplotlib.pyplot as plt
>>> al = ok.AssetList(['GC.COMM', 'FNER.INDX'], first_date='2000-01', last_date='2021-01')
>>> al.names
{'GC.COMM': 'Gold',
'FNER.INDX': 'FTSE NAREIT All Equity REITs'}
>>> al.kurtosis.plot()
>>> plt.show()

../_images/okama-EfficientFrontier-16.png

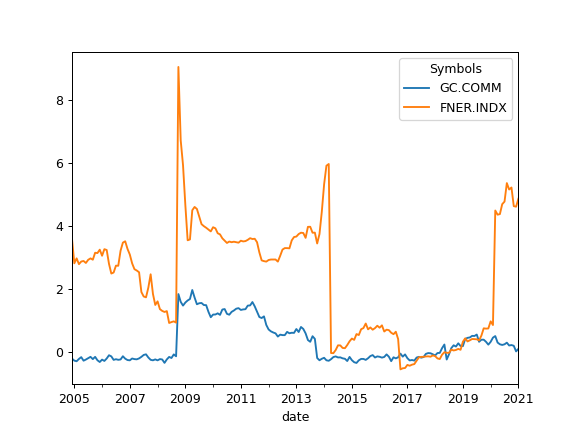
kurtosis_rolling(window=60)

Calculate rolling Fisher (normalized) kurtosis of the return time series for each asset.

Kurtosis is the fourth central moment divided by the square of the variance. It is a measure of the “tailedness” of the probability distribution of a real-valued random variable.

Kurtosis should be close to zero for normal distribution.

Parameters:

windowint, default 60: Rolling window size in months. This is the number of observations used for calculating the statistic. The window size should be at least 12 months.

Returns:

DataFrame: Rolling kurtosis time series for each asset.

See also

skewness: Compute skewness.
skewness_rolling: Compute rolling skewness.
kurtosis: Calculate expanding Fisher (normalized) kurtosis.
jarque_bera: Perform Jarque-Bera test for normality.
kstest: Perform Kolmogorov-Smirnov test for different types of distributions.

Examples

>>> import matplotlib.pyplot as plt
>>> al = ok.AssetList(['GC.COMM', 'FNER.INDX'], first_date='2000-01', last_date='2021-01')
>>> al.names
{'GC.COMM': 'Gold',
'FNER.INDX': 'FTSE NAREIT All Equity REITs'}
>>> al.kurtosis_rolling(window=12*5).plot()
>>> plt.show()

../_images/okama-EfficientFrontier-17.png

property mean_return

Calculate annualized mean return (arithmetic mean) for the rate of return time series (each asset).

Mean return calculated for the full history period. Arithmetic mean for the inflation is also shown if there is an inflation=True option in AssetList.

Returns:

Series: Mean return value for each asset.

Examples

>>> x = ok.AssetList(['MCFTR.INDX', 'RGBITR.INDX'], ccy='RUB', inflation=True)
>>> x.mean_return
MCFTR.INDX     0.209090
RGBITR.INDX    0.100133
dtype: float64

plot_assets(kind='mean', tickers='tickers', pct_values=False, xy_text=(0, 10))

Plot the assets points on the risk-return chart with annotations.

Annualized values for risk and return are used. Risk is a standard deviation of monthly rate of return time series. Return can be an annualized mean return (expected return) or CAGR (Compound annual growth rate).

Parameters:

kind{‘mean’, ‘cagr’}, default ‘mean’: Type of Return: annualized mean return (expected return) or CAGR (Compound annual growth rate).
tickers{‘tickers’, ‘names’} or list of str, default ‘tickers’: Annotation type for assets. ‘tickers’ - assets symbols are shown in form of ‘SPY.US’ ‘names’ - assets names are used like - ‘SPDR S&P 500 ETF Trust’ To show custom annotations for each asset pass the list of names.
pct_valuesbool, default False: Risk and return values in the axes: Algebraic annotation (False) Percents (True)
xy_texttuple, default (0, 10): The shift of the annotation text (x, y) from the point.

Returns:

Axes‘matplotlib.axes._subplots.AxesSubplot’

Examples

>>> import matplotlib.pyplot as plt
>>> al = ok.AssetList(['SPY.US', 'AGG.US'], ccy='USD', inflation=False)
>>> al.plot_assets()
>>> plt.show()

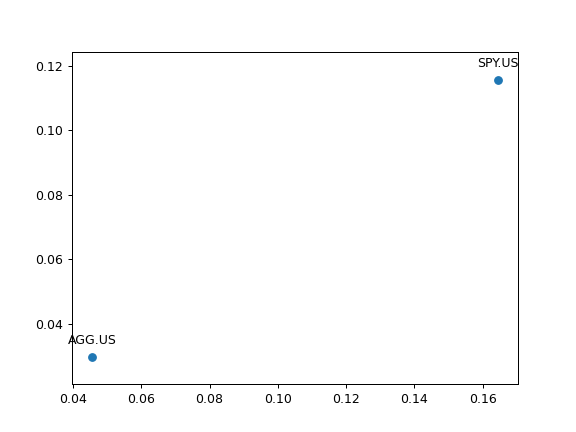
../_images/okama-EfficientFrontier-18_00_00.png

Plotting with default parameters values shows expected return, ticker annotations and algebraic values for risk and return. To use CAGR instead of expected return use kind=’cagr’.

>>> al.plot_assets(kind='cagr',
...               tickers=['US Stocks', 'US Bonds'],  # use custom annotations for the assets
...               pct_values=True  # risk and return values are in percents
...               )
>>> plt.show()

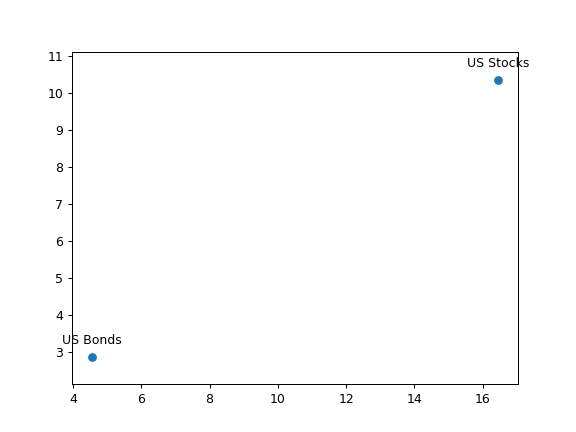
../_images/okama-EfficientFrontier-18_01_00.png

plot_pair_ef(tickers='tickers', figsize=None)

Plot Efficient Frontier of every pair of assets.

Efficient Frontier is a set of portfolios which satisfy the condition that no other portfolio exists with a higher expected return but with the same risk (standard deviation of return).

Arithmetic mean (expected return) is used for optimized portfolios.

Parameters:

tickers{‘tickers’, ‘names’} or list of str, default ‘tickers’: Annotation type for assets. ‘tickers’ - assets symbols are shown in form of ‘SPY.US’ ‘names’ - assets names are used like - ‘SPDR S&P 500 ETF Trust’ To show custom annotations for each asset pass the list of names.
figsize: (float, float), optional: Figure size: width, height in inches. If None default matplotlib size is taken: [6.4, 4.8]

Returns:

Axes‘matplotlib.axes._subplots.AxesSubplot’

Notes

It should be at least 3 assets.

Examples

>>> import matplotlib.pyplot as plt
>>> ls4 = ['SPY.US', 'BND.US', 'GLD.US', 'VNQ.US']
>>> curr = 'USD'
>>> last_date = '07-2021'
>>> ef = ok.EfficientFrontier(ls4, ccy=curr, last_date=last_date)
>>> ef.plot_pair_ef()
>>> plt.show()

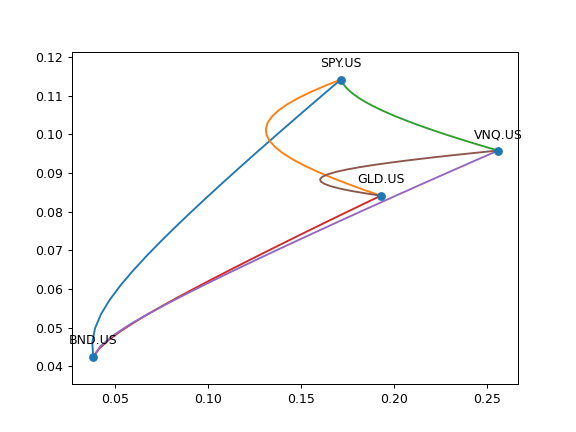
../_images/okama-EfficientFrontier-19_00_00.png

It can be useful to plot the full Efficent Frontier (EF) with optimized 4 assets portfolios together with the EFs for each pair of assets.

>>> ef4 = ok.EfficientFrontier(assets=ls4, ccy=curr, n_points=100)
>>> df4 = ef4.ef_points
>>> fig = plt.figure()
>>> # Plot Efficient Frontier of every pair of assets. Optimized portfolios will have 2 assets.
>>> ef4.plot_pair_ef()  # mean return is used for optimized portfolios.
>>> ax = plt.gca()
>>> # Plot the full Efficient Frontier for 4 asset portfolios.
>>> ax.plot(df4['Risk'], df4['Mean return'], color = 'black', linestyle='--')
>>> plt.show()

../_images/okama-EfficientFrontier-19_01_00.png

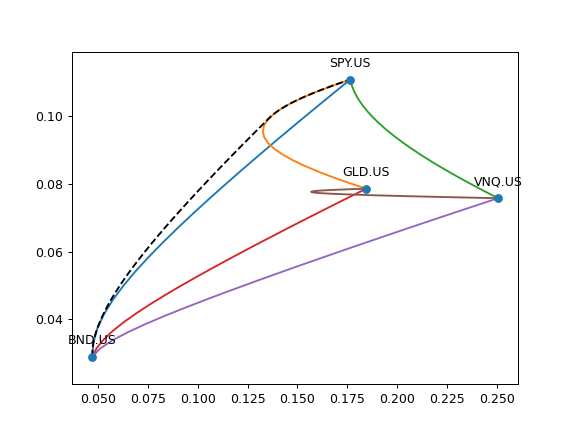
../_images/okama-EfficientFrontier-19_01_01.png

property real_mean_return

Calculate annualized real mean return (arithmetic mean) for the rate of return time series (each assets).

Real rate of return is adjusted for inflation. Real return is defined if there is an inflation=True option in AssetList.

Returns:

Series: Mean real return value for each asset.

Examples

>>> x = ok.AssetList(['MCFTR.INDX', 'RGBITR.INDX'], ccy='RUB', inflation=True)
>>> x.real_mean_return
MCFTR.INDX     0.118116
RGBITR.INDX    0.017357
dtype: float64

property recovery_periods

Calculate the longest recovery periods for the assets.

The recovery period (drawdown duration) is the number of months to reach the value of the last maximum.

Returns:

Series: Max recovery period for each asset (in months).

See also

drawdowns: Calculate drawdowns time series.

Notes

If the last asset maximum value is not recovered NaN is returned. The largest recovery period does not necessary correspond to the max drawdown.

Examples

>>> x = ok.AssetList(['SPY.US', 'AGG.US'])
>>> x.recovery_periods
SPY.US    52
AGG.US    15
dtype: int32

property risk_annual

Calculate annualized risk expanding time series for each asset.

Risk is a standard deviation of the rate of return.

Annualized risk time series is calculated for the rate of return from ‘first_date’ to ‘last_date’ (expanding).

Returns:

DataFrame: Annualized risk (standard deviation) expanding time series for each asset.

See also

risk_monthly: Calculate montly risk expanding time series for each asset.
get_rolling_risk_annual: Calculate annualized risk rolling time series.
semideviation_monthly: Calculate semideviation monthly values.
semideviation_annual: Calculate semideviation annualized values.
get_var_historic: Calculate historic Value at Risk (VaR).
get_cvar_historic: Calculate historic Conditional Value at Risk (CVaR).
drawdowns: Calculate assets drawdowns.

Notes

CFA recomendations are used to annualize risk values [1].

[1]

What’s Wrong with Multiplying by the Square Root of Twelve. Paul D. Kaplan, CFA Institute Journal Review, 2013

Examples

>>> al = ok.AssetList(['GC.COMM', 'SHV.US'], ccy='USD', last_date='2021-01')
>>> al.risk_annual
GC.COMM    0.195236
SHV.US     0.004960
dtype: float64

property risk_monthly

Calculate monthly risk expanding time series for each asset.

Monthly risk of the asset is a standard deviation of the rate of return time series. Standard deviation (sigma σ) is normalized by N-1.

Monthly risk is calculated for the rate of retirun time series for the sample from ‘first_date’ to ‘last_date’.

Returns:

DataFrame: Monthly risk (standard deviation) expanding time series for each asset in form of Series.

See also

risk_annual: Calculate annualized risks expanding time series.
semideviation_monthly: Calculate semideviation monthly values.
semideviation_annual: Calculate semideviation annualized values.
get_var_historic: Calculate historic Value at Risk (VaR).
get_cvar_historic: Calculate historic Conditional Value at Risk (CVaR).
drawdowns: Calculate drawdowns.

Examples

>>> al = ok.AssetList(['GC.COMM', 'SHV.US'], ccy='USD', last_date='2021-01')
>>> al.risk_monthly
Symbols   GC.COMM    SHV.US
date
2007-03  0.025668  0.000141
2007-04  0.020872  0.000153
2007-05  0.027513  0.000451
2007-06  0.025988  0.000406
           ...       ...
2020-09  0.051006  0.001380
2020-10  0.050861  0.001377

property semideviation_annual

Return semideviation annualized values for each asset.

Semi-deviation (Downside risk) is the risk of the return being below the expected return.

Semi-deviation is calculated for rate of retirun time series for the sample from ‘first_date’ to ‘last_date’.

Returns:

Series: Annualized semideviation values for each asset in form of Series.

See also

risk_monthly: Calculate montly risk for each asset.
risk_annual: Calculate annualized risks.
semideviation_monthly: Calculate semideviation monthly values.
get_var_historic: Calculate historic Value at Risk (VaR).
get_cvar_historic: Calculate historic Conditional Value at Risk (CVaR).
drawdowns: Calculate drawdowns.

Examples

>>> al = ok.AssetList(['GC.COMM', 'SHV.US'], ccy='USD', last_date='2021-01')
>>> al.semideviation_annual
GC.COMM    0.115302
SHV.US     0.000560
dtype: float64

property semideviation_monthly

Calculate semi-deviation monthly values for each asset.

Semi-deviation (Downside risk) is the risk of the return being below the expected return.

Semi-deviation is calculated for rate of retirun time series for the sample from ‘first_date’ to ‘last_date’.

Returns:

Series: Monthly semideviation values for each asset in form of Series.

See also

risk_monthly: Calculate montly risk for each asset.
risk_annual: Calculate annualized risks.
semideviation_annual: Calculate semideviation annualized values.
get_var_historic: Calculate historic Value at Risk (VaR).
get_cvar_historic: Calculate historic Conditional Value at Risk (CVaR).
drawdowns: Calculate drawdowns.

Examples

>>> al = ok.AssetList(['GC.COMM', 'SHV.US'], ccy='USD', last_date='2021-01')
>>> al.semideviation_monthly
GC.COMM    0.039358
SHV.US     0.000384
dtype: float64

property skewness

Compute expanding skewness of the return time series for each asset returns.

Skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined.

For normally distributed returns, the skewness should be about zero. A skewness value greater than zero means that there is more weight in the right tail of the distribution.

Returns:

Dataframe: Expanding skewness time series for each asset.

See also

skewness_rolling: Compute rolling skewness.
kurtosis: Calculate expanding Fisher (normalized) kurtosis.
kurtosis_rolling: Calculate rolling Fisher (normalized) kurtosis.
jarque_bera: Perform Jarque-Bera test for normality.
kstest: Perform Kolmogorov-Smirnov test for different types of distributions.

Examples

>>> import matplotlib.pyplot as plt
>>> al = ok.AssetList(['VFINX.US', 'GC.COMM'], last_date='2021-01')
>>> al.names
{'VFINX.US': 'VANGUARD 500 INDEX FUND INVESTOR SHARES',
'GC.COMM': 'Gold'}
>>> al.skewness.plot()
>>> plt.show()

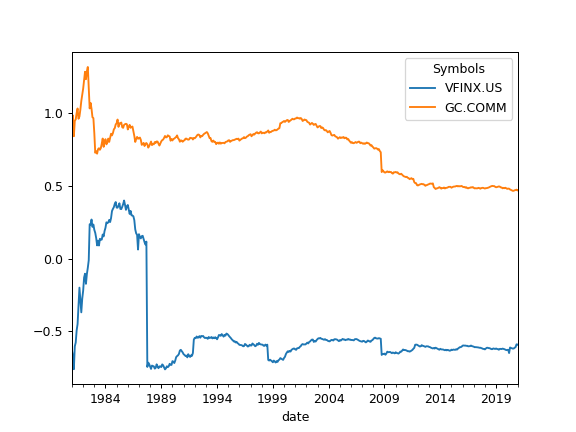
../_images/okama-EfficientFrontier-20.png

skewness_rolling(window=60)

Compute rolling skewness of the return time series for each asset.

Skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined.

For normally distributed returns, the skewness should be about zero. A skewness value greater than zero means that there is more weight in the right tail of the distribution.

Parameters:

windowint, default 60: Rolling window size in months. This is the number of observations used for calculating the statistic. The window size should be at least 12 months.

Returns:

DataFrame: Rolling skewness time series for each asset.

See also

skewness: Compute skewness.
kurtosis: Calculate expanding Fisher (normalized) kurtosis.
kurtosis_rolling: Calculate rolling Fisher (normalized) kurtosis.
jarque_bera: Perform Jarque-Bera test for normality.
kstest: Perform Kolmogorov-Smirnov test for different types of distributions.

Examples

>>> import matplotlib.pyplot as plt
>>> al = ok.AssetList(['VFINX.US', 'GC.COMM'], last_date='2021-01')
>>> al.names
{'VFINX.US': 'VANGUARD 500 INDEX FUND INVESTOR SHARES',
'GC.COMM': 'Gold'}
>>> al.skewness_rolling(window=12*5).plot()
>>> plt.show()

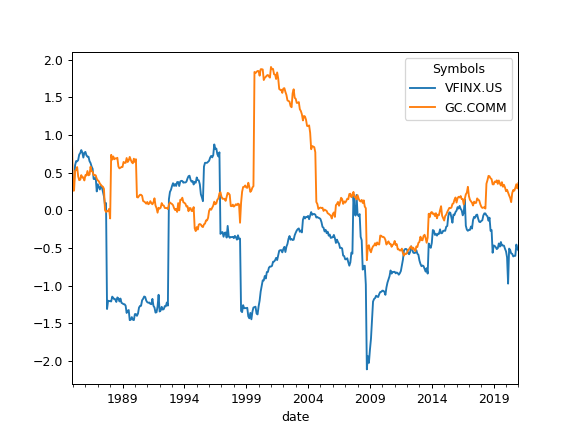
../_images/okama-EfficientFrontier-21.png

property symbols

Return a list of financial symbols used to set the AssetList.

Symbols are similar to tickers but have a namespace information:

SPY.US is a symbol
SPY is a ticker

Returns:

list of str: List of symbols included in the Asset List.

property tickers

Return a list of tickers (symbols without a namespace) used to set the AssetList.

tickers are similar to symbols but do not have namespace information:

SPY is a ticker
SPY.US is a symbol

Returns:

list of str: List of tickers included in the Asset List.

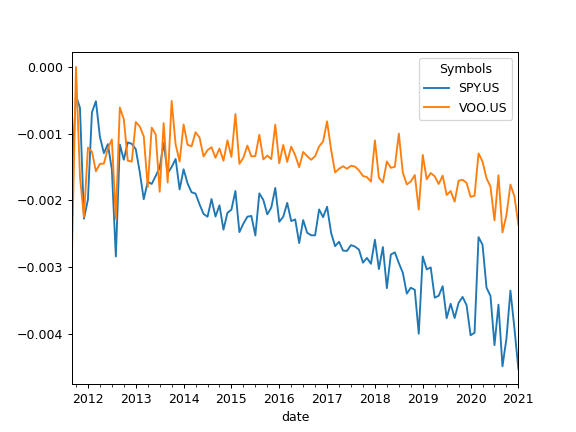
tracking_difference(rolling_window=None)

Return tracking difference for the rate of return of assets.

Tracking difference is calculated by measuring the accumulated difference between the returns of a benchmark and those of the ETF replicating it (could be mutual funds, or other types of assets). Tracking difference is measured in percents.

Benchmark should be in the first position of the symbols list in AssetList parameters.

Parameters:

rolling_windowint or None, default None: Size of the moving window in months. If None calculate expanding tracking difference.

Returns:

DataFrame: Tracking diffirence time series for each asset.

Examples

>>> import matplotlib.pyplot as plt
>>> x = ok.AssetList(['SP500TR.INDX', 'SPY.US', 'VOO.US'], last_date='2021-01')
>>> x.tracking_difference().plot()
>>> plt.show()

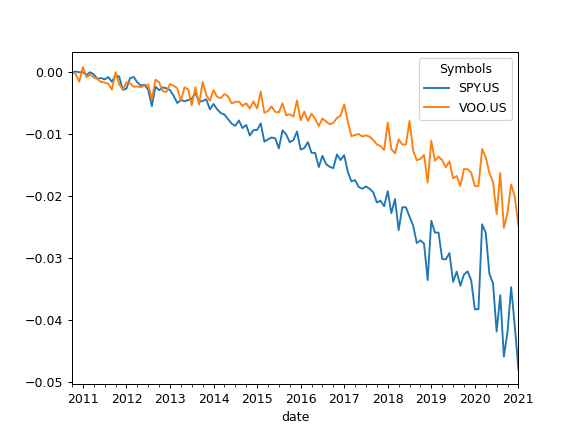
../_images/okama-EfficientFrontier-22_00_00.png

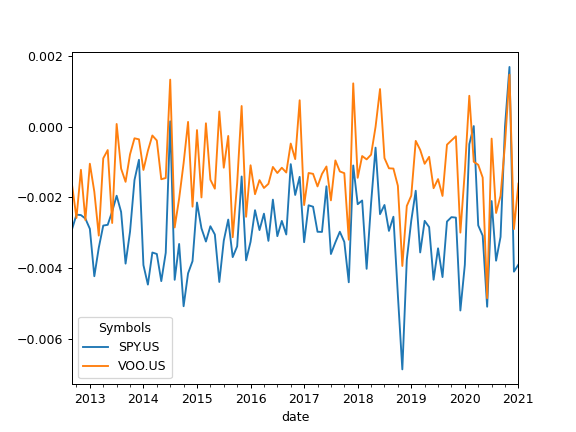
To calculate rolling Tracking difference set rolling_window to a number of months (moving window size):

>>> x.tracking_difference(rolling_window = 24).plot()
>>> plt.show()

../_images/okama-EfficientFrontier-22_01_00.png

property tracking_difference_annual

Calculate tracking difference for each calendar year.

Tracking difference is calculated by measuring the accumulated difference between the returns of a benchmark and ETFs replicating it (could be mutual funds, or other types of assets). Tracking difference is measured in percents.

Benchmark should be in the first position of the symbols list in AssetList parameters.

Returns:

DataFrame: Time series with tracking difference for each calendar year period.

Examples

>>> import matplotlib.pyplot as plt
>>> al = ok.AssetList(['SP500TR.INDX', 'VOO.US', 'SPXS.LSE'], inflation=False)
>>> al.tracking_difference_annual.plot(kind='bar')

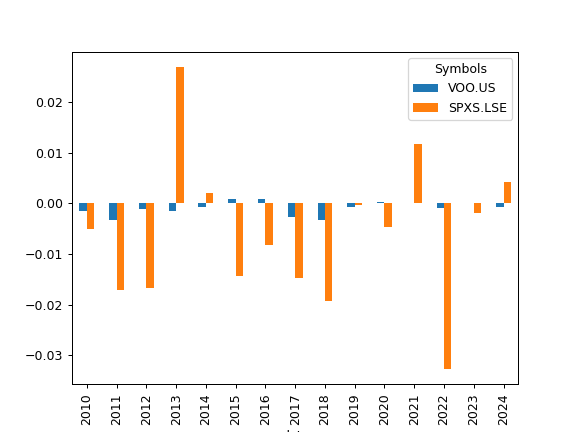
../_images/okama-EfficientFrontier-23.png

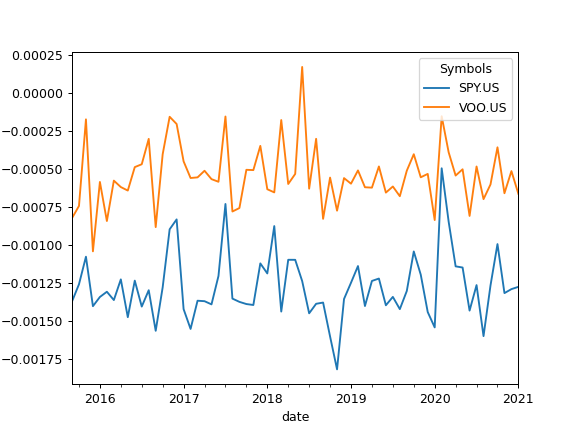
tracking_difference_annualized(rolling_window=None)

Calculate annualized tracking difference time series for the rate of return of assets.

Tracking difference is calculated by measuring the accumulated difference between the returns of a benchmark and ETFs replicating it (could be mutual funds, or other types of assets). Tracking difference is measured in percents.

Benchmark should be in the first position of the symbols list in AssetList parameters.

Annual values are available for history periods of more than 12 months. Returns for less than 12 months can’t be annualized According to the CFA Institute’s Global Investment Performance Standards (GIPS).

Parameters:

rolling_windowint or None, default None: Size of the moving window in months. Must be at least 12 months. If None calculate expanding annualized tracking difference.

Returns:

DataFrame: Annualized tracking diffirence time series for each asset.

Examples

>>> import matplotlib.pyplot as plt
>>> x = ok.AssetList(['SP500TR.INDX', 'SPY.US', 'VOO.US'], last_date='2021-01')
>>> x.tracking_difference_annualized().plot()

To calculate rolling annualized tracking difference set rolling_window to a number of months (moving window size):

>>> x.tracking_difference_annualized(rolling_window = 12*5).plot()
>>> plt.show()

../_images/okama-EfficientFrontier-24_00.png

../_images/okama-EfficientFrontier-24_01.png

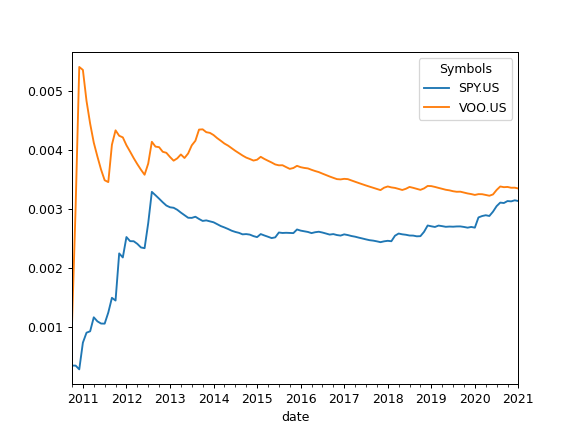
tracking_error(rolling_window=None)

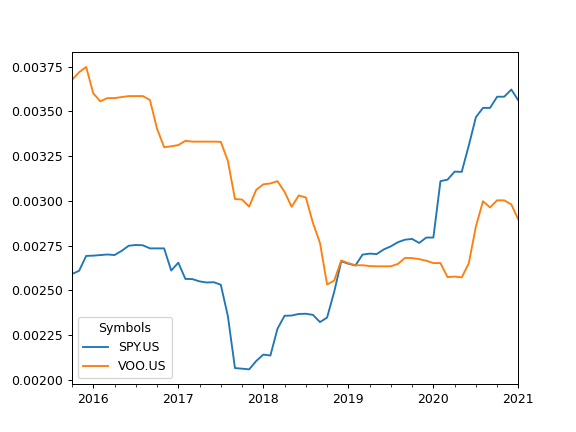
Calculate tracking error time series for the rate of return of assets.

Tracking error is defined as the standard deviation of the difference between the returns of the asset and the returns of the benchmark. Tracking error is measured in percents.

Benchmark should be in the first position of the symbols list in AssetList parameters.

Parameters:

rolling_windowint or None, default None: Size of the moving window in months. Must be at least 12 months. If None calculate expanding tracking error.

Returns:

DataFrame: rolling or expanding tracking error time series for each asset.

Examples

>>> import matplotlib.pyplot as plt
>>> x = ok.AssetList(['SP500TR.INDX', 'SPY.US', 'VOO.US'], last_date='2021-01')
>>> x.tracking_error().plot()
>>> plt.show()

../_images/okama-EfficientFrontier-25_00_00.png

To calculate rolling tracking error set rolling_window to a number of months (moving window size):

>>> x.tracking_error(rolling_window = 12*5).plot()
>>> plt.show()

../_images/okama-EfficientFrontier-25_01_00.png

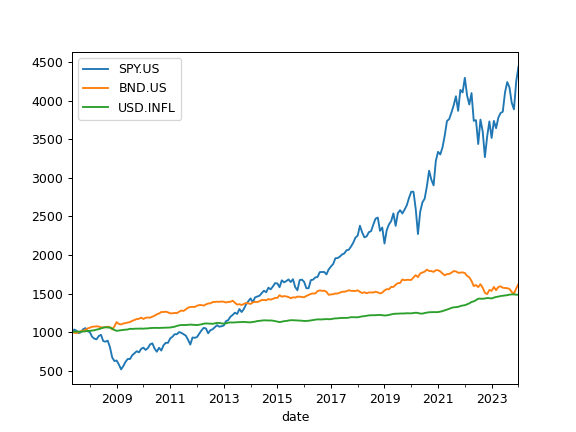
property wealth_indexes

Calculate wealth index time series for the assets and accumulated inflation.

Wealth index (Cumulative Wealth Index) is a time series that presents the value of each asset over historical time period. Accumulated inflation time series is added if inflation=True in the AssetList.

Wealth index is obtained from the accumulated return multiplicated by the initial investments. That is: 1000 * (Acc_Return + 1) Initial investments are taken as 1000 units of the AssetList base currency.

Returns:

DataFrame: Time series of wealth index values for each asset and accumulated inflation.

Examples

>>> import matplotlib.pyplot as plt
>>> x = ok.AssetList(['SPY.US', 'BND.US'])
>>> x.wealth_indexes.plot()
>>> plt.show()

../_images/okama-EfficientFrontier-26.png

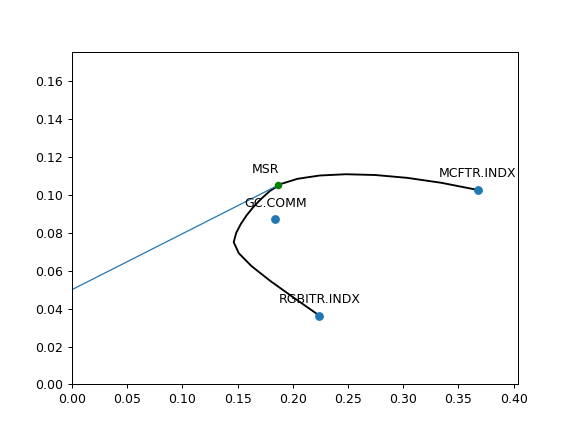
plot_cml(rf_return=0, y_axe='cagr', figsize=None)

Plot Capital Market Line (CML).

The Capital Market Line (CML) is the tangent line drawn from the point of the risk-free asset (volatility is zero) to the point of tangency portfolio or Maximum Sharpe Ratio (MSR) point.

The slope of the CML is the Sharpe ratio of the tangency portfolio.

Parameters:

rf_returnfloat, default 0: Risk-free rate of return.
y_axe{‘cagr’, ‘mean_return’}, default ‘cagr’: Show the relation between Risk and CAGR (if ‘cagr’) or between Risk and Mean rate of return (if ‘mean_return’). CAGR or Mean Rate of Return are displayed on the y-axis.
figsize(float, float), optional: Figure size: width, height in inches. If None default matplotlib size is taken: [6.4, 4.8]

Returns:

Axes‘matplotlib.axes._subplots.AxesSubplot’

Examples

>>> import matplotlib.pyplot as plt
>>> three_assets = ['MCFTR.INDX', 'RGBITR.INDX', 'GC.COMM']
>>> ef = ok.EfficientFrontier(assets=three_assets, ccy='USD', full_frontier=True)
>>> ef.plot_cml(rf_return=0.05, y_axe="cagr")  # Risk-Free return is 5%
>>> plt.show

../_images/okama-EfficientFrontier-27.png